A new MOX Report entitled “A Necas-Lions inequality with symmetric gradients on star-shaped domains based on a first order Babuska-Aziz inequality” by Botti, M.; Mascotto, L. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/52-2024.pdf Abstract: We prove a Necas-Lions inequality with symmetric gradients on two and three dimensional domains that are star-shaped with respect to a ball B; the constants in the inequality are explicit with respect to the diameter and the radius of B. Crucial tools in deriving this inequality are a first order Babuska-Aziz inequality based on Bogovskii’s construction of a right-inverse of the divergence and Fourier transform techniques proposed by Duran. As a byproduct, we derive arbitrary order estimates in arbitrary dimension for that operator.
You may also like
A new MOX Report entitled “Polytopal discontinuous Galerkin methods for low-frequency poroelasticity coupled to unsteady Stokes flow” by Botti, M.; Fumagalli, I.; […]
A new MOX Report entitled ” Modeling Hypoxia Induced Radiation Resistance and the Impact of Radiation Sources ” by Possenti, L.; Vitullo, […]
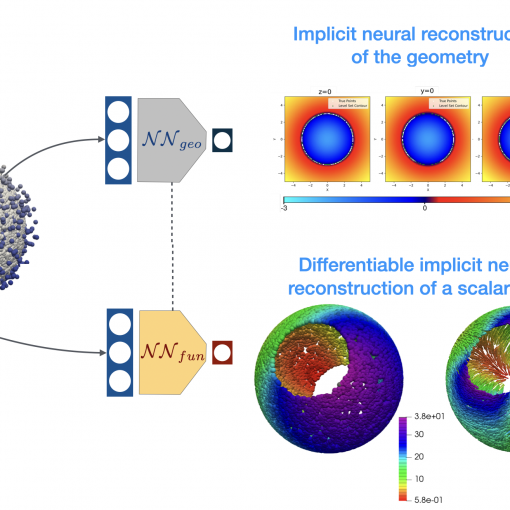
A new MOX Report entitled “Implicit neural field reconstruction on complex shapes from scattered and noisy data” by Carrara, D.; Regazzoni, F.; […]
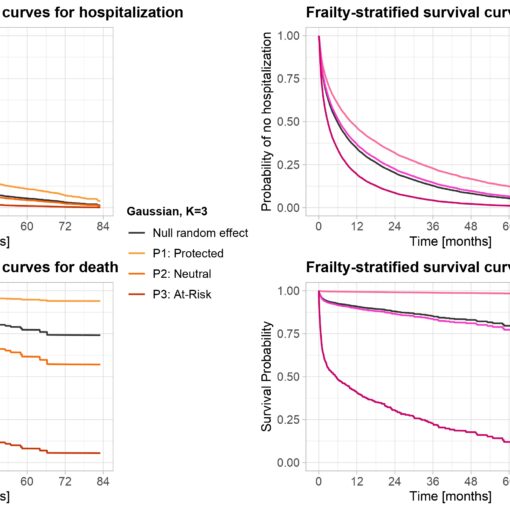
A new MOX Report entitled “Joint modelling of recurrent and terminal events with discretely-distributed non-parametric frailty: application on re-hospitalizations and death in […]