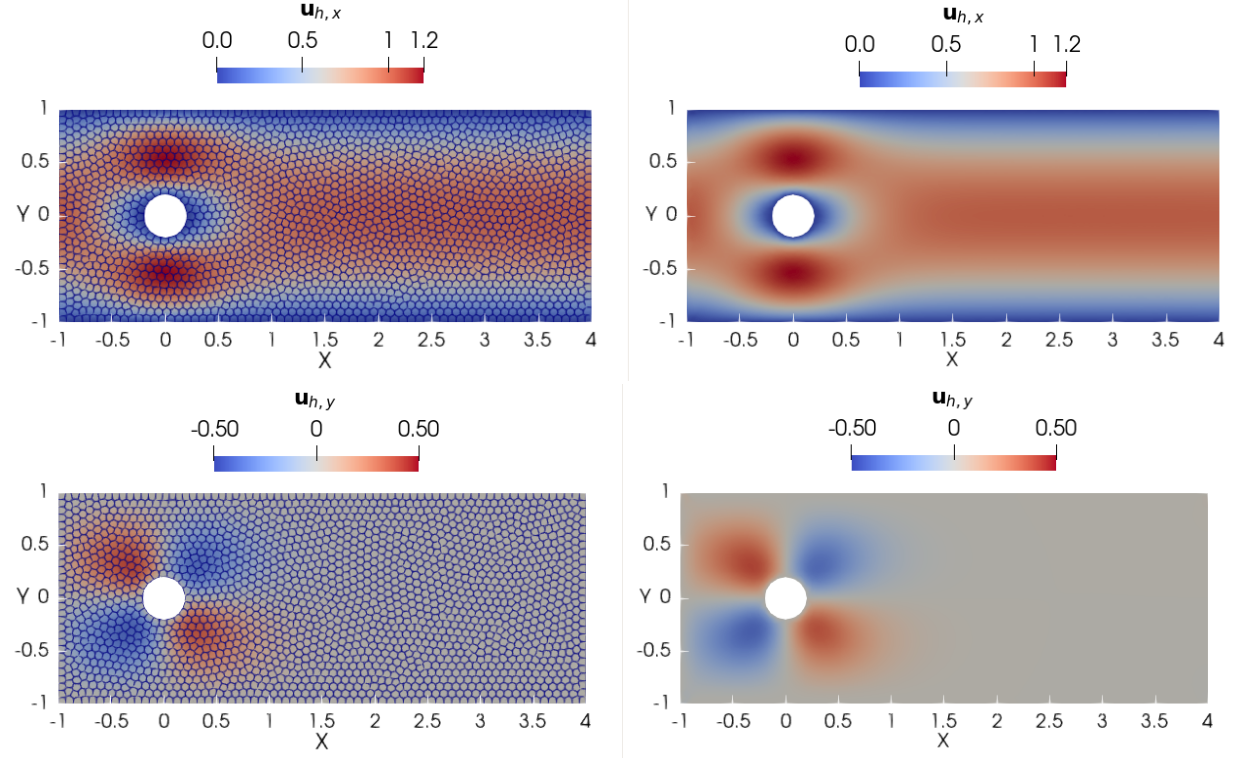
A new MOX Report entitled “A polytopal discontinuous Galerkin method for the pseudo-stress formulation of the unsteady Stokes problem” by Antonietti, P.F.; Botti, M.; Cancrini, A.; Mazzieri, I. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/54-2024.pdf Abstract: This work aims to construct and analyze a discontinuous Galerkin method on polytopal grids (PolydG) to solve the pseudo-stress formulation of the unsteady Stokes problem. The pseudo-stress variable is introduced due to the growing interest in non-Newtonian flows and coupled interface problems, where stress assumes a fundamental role. The space-time discretization of the problem is achieved by combining the PolydG approach with the implicit theta-method time integration scheme. For both the semi- and fully-discrete problems we present a detailed stability analysis. Moreover, we derive convergence estimates for the fully discrete space-time discretization. A set of verification tests is presented to verify the theoretical estimates and the application of the method to cases of engineering interest.
You may also like
A new MOX Report entitled “A Necas-Lions inequality with symmetric gradients on star-shaped domains based on a first order Babuska-Aziz inequality” by […]
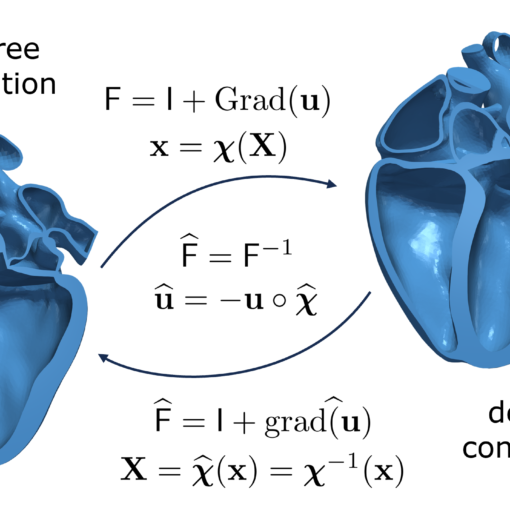
A new MOX Report entitled “Reconstructing relaxed configurations in elastic bodies: mathematical formulation and numerical methods for cardiac modeling” by Barnafi, N. […]
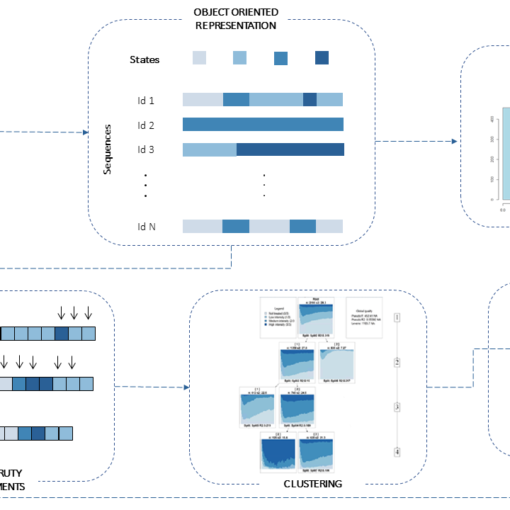
A new MOX Report entitled “Capturing the variety of clinical pathways in patients with schizophrenic disorders through state sequences analysis” by Savaré, […]
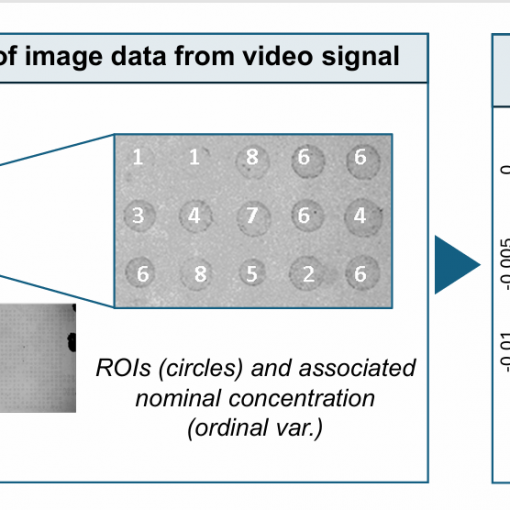
A new MOX Report entitled “Functional-Ordinal Canonical Correlation Analysis With Application to Data from Optical Sensors” by Patanè, G.; Nicolussi, F.; Krauth, […]