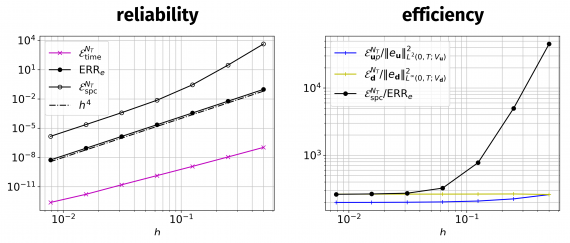
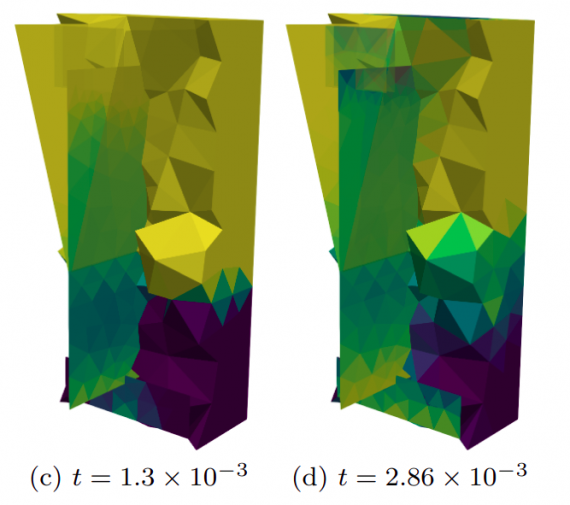
A new MOX Report entitled “A discontinuous Galerkin method for the three-dimensional heterodimer model with application to prion-like proteins’ dynamics” by Antonietti, P.F.; Corti, M.; Lorenzon, G. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/51-2024.pdf Abstract: Neurocognitive disorders, such as Alzheimer’s and Parkinson’s, have a wide […]
admin
A new MOX Report entitled “A posteriori error analysis for a coupled Stokes-poroelastic system with multiple compartments” by Fumagalli, I.; Parolini, N.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/50-2024.pdf Abstract: The computational effort entailed in the discretization of fluid-poromechanics systems is typically highly […]
A new MOX Report entitled ” A hybrid upwind scheme for two-phase flow in fractured porous media ” by Ballini, E.; Formaggia, L.; Fumagalli, A.; Keilegavlen, E.; Scotti, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/49-2024.pdf Abstract: Simulating the flow of two fluid phases in […]
A new MOX Report entitled “Addressing Atmospheric Absorption in Adaptive Rectangular Decomposition” by Cicalese, G.; Ciaramella, G.; Mazzieri, I. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/48-2024.pdf Abstract: This paper focuses on the Adaptive Rectangular Decomposition (ARD) scheme, a wave-based method utilized for acoustic simulations. ARD […]
We are thrilled to welcome you to the hashtag#HPCSIM2024 Conference at Politecnico di Milano. Join us in the Roger Room for insightful talks and networking opportunities with leading experts in high-performance computing! HPCSIM24 is organized by MOX Laboratory – Politecnico di Milano, ICEA Dipartimento di Ingegneria Civile Edile e Ambientale […]
The Italian Society of Applied and Industrial Mathematics (SIMAI) awarded Francesco Regazzoni the Young Researcher Prize 2024. The Prize is awarded to researchers up to 35 years of age, based on: autonomy in the scientific production, capability of developing lines of research of interest to applications of mathematics, international recognition, […]
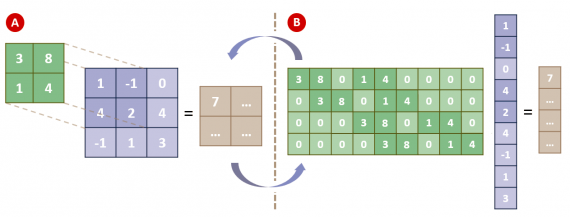
A new MOX Report entitled “A practical existence theorem for reduced order models based on convolutional autoencoders” by Franco, N.R.; Brugiapaglia, S. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/47-2024.pdf Abstract: In recent years, deep learning has gained increasing popularity in the fields of Partial Differential […]
Michel Bucelli has been awarded the prestigious ECCOMAS 2024 PhD Olympiad prize with his presentation “Mathematical and Numerical Modeling of the Heart Function: Integrating Electrophysiology, Mechanics and Fluid Dynamics”. The prize had been awarded during the ECCOMAS 2024 Congress in Lisbon (https://eccomas2024.org/)
The Italian Society of Statistics (SIS) awarded Prof. Francesca Ieva the “Award to Young Scholars for Contributions to Statistical Disciplines”, 2024 edition, with the following motivation: “The prize committee proposed to award the prize for the year 2024 to SIS member Francesca Ieva, whose broad scientific production stands out for its […]
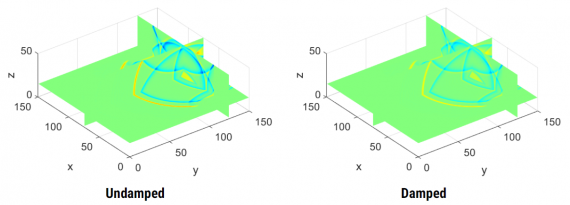
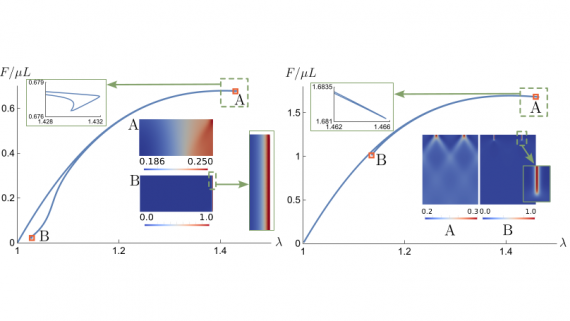
A new MOX Report entitled “Elastic Instability behind Brittle Fracture” by Riccobelli, D.; Ciarletta, P.; Vitale, G.; Maurini, C.; Truskinovsky, L. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/46-2024.pdf Abstract: We argue that nucleation of brittle cracks in initially flawless soft elastic solids is preceded by […]