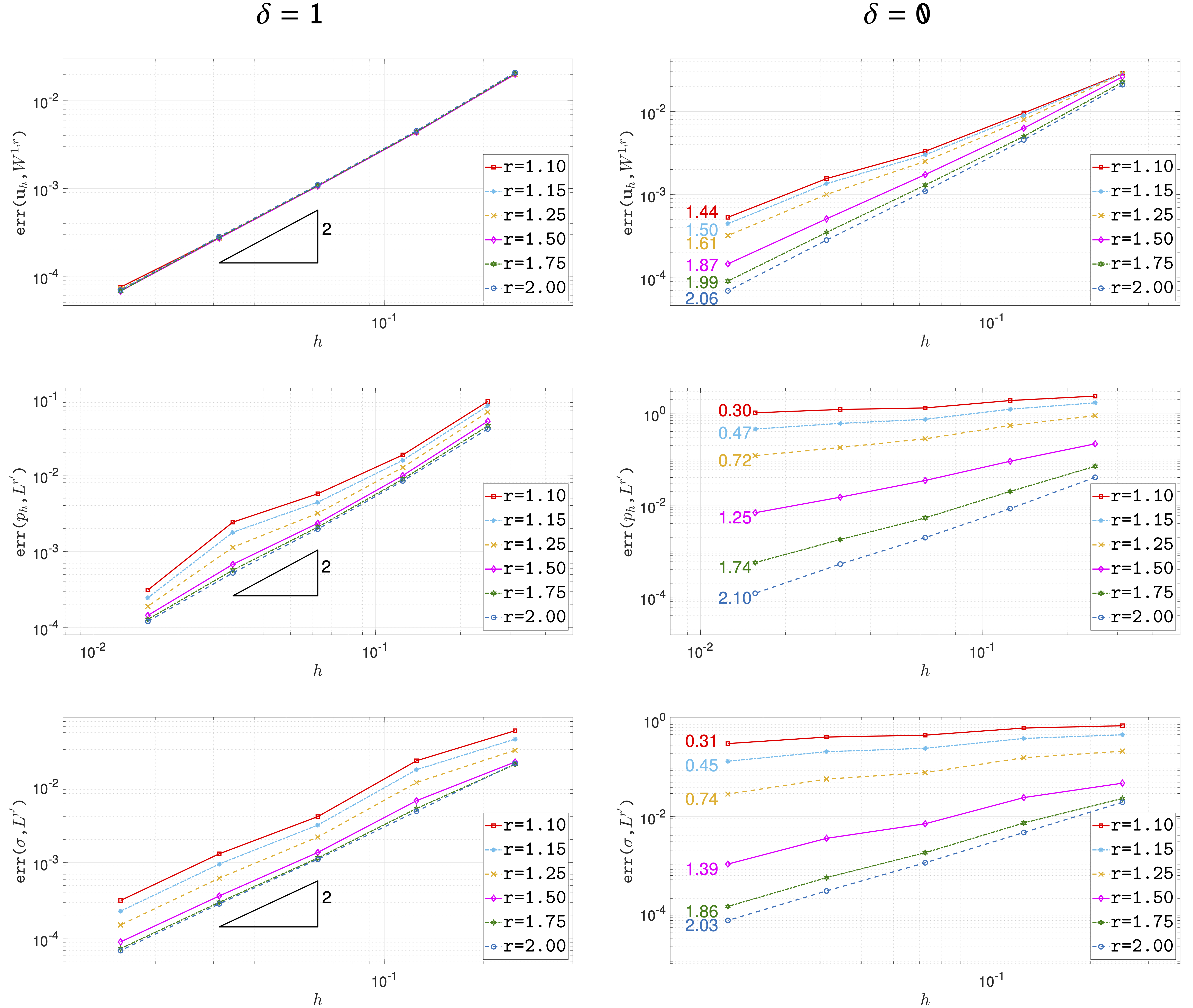
A new MOX Report entitled “A Virtual Element method for non-Newtonian fluid flows” by Antonietti, P.F.; Beirao da Veiga, L.; Botti, M.; Vacca, G.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/27-2024.pdf Abstract: In this paper, we design and analyze a Virtual Element discretization for the steady motion of non-Newtonian, incompressible fluids. A specific stabilization, tailored to mimic the monotonicity and boundedness properties of the continuous operator, is introduced and theoretically investigated. The proposed method has several appealing features, including the exact enforcement of the divergence free condition and the possibility of making use of fully general polygonal meshes. A complete well-posedness and convergence analysis of the proposed method is presented under mild assumptions on the non-linear laws, encompassing common examples such as the Carreau–Yasuda model. Numerical experiments validating the theoretical bounds as well as demonstrating the practical capabilities of the proposed formulation are presented.
You may also like
A new MOX Report entitled “Nonparametric tests for semiparametric regression models” by Ferraccioli, F.; Sangalli, L.M.; Finos, L. has appeared in the […]
A new MOX Report entitled “A comprehensive stroke risk assessment by combining atrial computational fluid dynamics simulations and functional patient data” by […]
A new MOX Report entitled “Modelling of initially stressed solids: structure of the energy density in the incompressible limit” by Magri, M.; […]
A new MOX Report entitled “Discontinuous Galerkin for the heterodimer model of prion dynamics in Parkinson’s disease” by Antonietti, P.F.; Bonizzoni, F.; […]