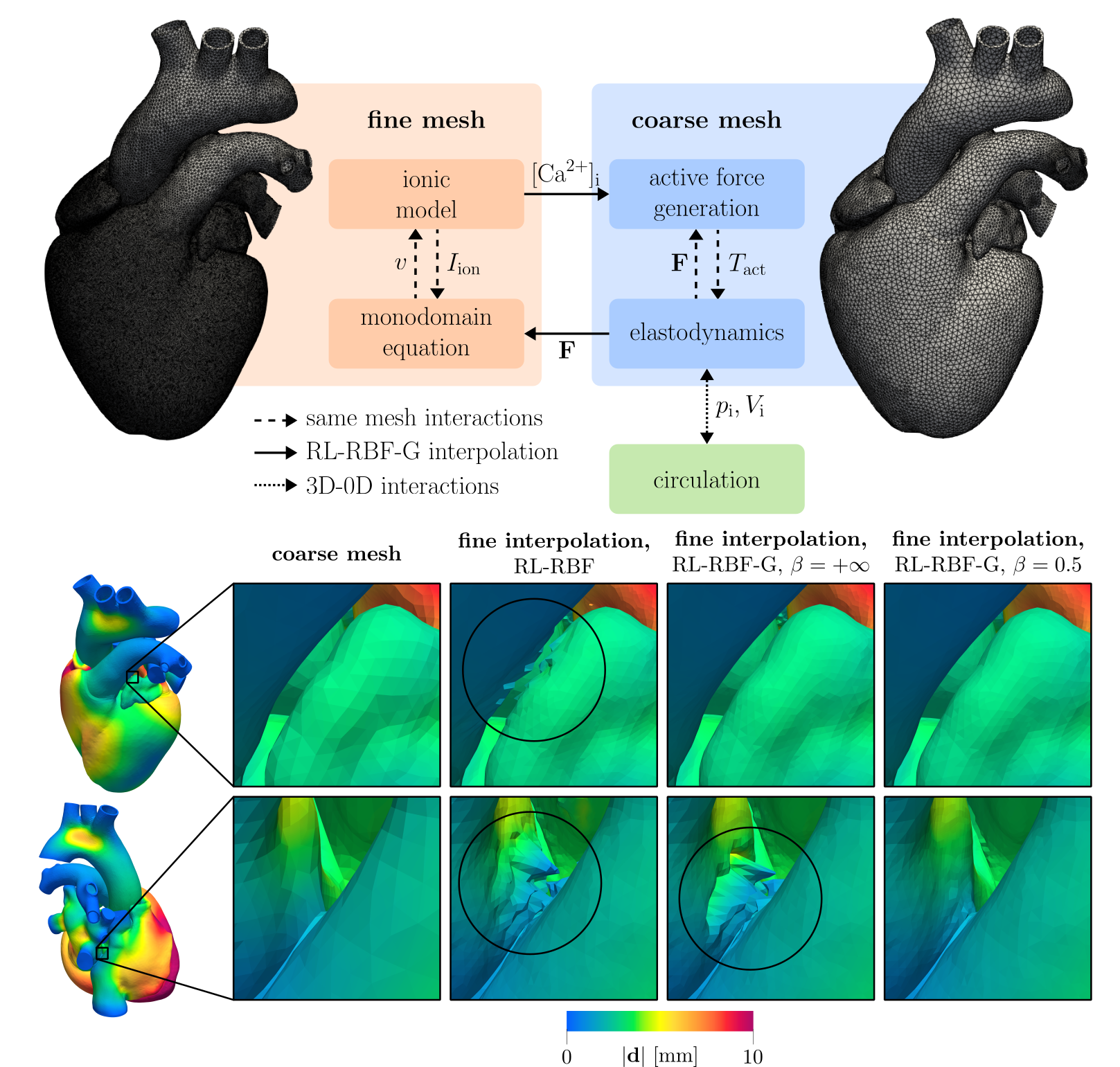
A new MOX Report entitled “Robust radial basis function interpolation based on geodesic distance for the numerical coupling of multiphysics problems” by Bucelli, M.; Regazzoni, F.; Dede’, L.; Quarteroni, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/26-2024.pdf Abstract: Multiphysics simulations frequently require transferring solution fields between subproblems with non-matching spatial discretizations, typically using interpolation techniques. Standard methods are usually based on measuring the closeness between points by means of the Euclidean distance, which does not account for curvature, cuts, cavities or other non-trivial geometrical or topological features of the domain. This may lead to spurious oscillations in the interpolant in proximity to these features. To overcome this issue, we propose a modification to rescaled localized radial basis function (RL-RBF) interpolation to account for the geometry of the interpolation domain, by yielding conformity and fidelity to geometrical and topological features. The proposed method, referred to as RL-RBF-G, relies on measuring the geodesic distance between data points. RL-RBF-G removes spurious oscillations appearing in the RL-RBF interpolant, resulting in incre! ased accu racy in domains with complex geometries. We demonstrate the effectiveness of RL-RBF-G interpolation through a convergence study in an idealized setting. Furthermore, we discuss the algorithmic aspects and the implementation of RL-RBF-G interpolation in a distributed-memory parallel framework, and present the results of a strong scalability test yielding nearly ideal results. Finally, we show the effectiveness of RL-RBF-G interpolation in multiphysics simulations by considering an application to a whole-heart cardiac electromecanics model.
