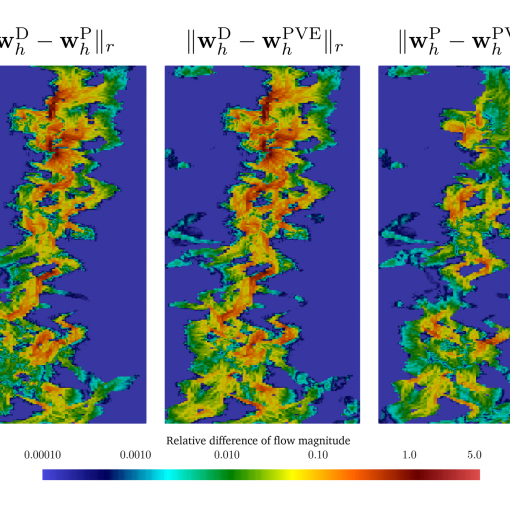
A new MOX Report entitled “Robust Preconditioning of Mixed-Dimensional PDEs on 3d-1d domains coupled with Lagrange Multipliers” by Dimola N.; Kuchta M.; Mardal K.A.; Zunino P. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/103-2023.pdf
Abstract: In the context of micro-circulation, the coexistence of two distinct length scales – the vascular radius and the tissue/organ scale – with a substantial difference in magnitude, poses significant challenges. To handle slender inclusions and simplify the geometry involved, a technique called topological dimensionality reduction is used, which suppresses the manifold dimensions associated with the smaller characteristic length. However, the algebraic structure of the resulting discretized system presents a challenge in constructing efficient solution algorithms. This chapter addresses this challenge by developing a robust preconditioner for the 3d-1d problem using the operator preconditioning technique. The robustness of the preconditioner is demonstrated with respect to the problem parameters, except for the vascular radius. The vascular radius, as demonstrated, plays a fundamental role in the mathematical well-posedness of the problem and the effectiveness of the preconditioner.