A new MOX Report entitled “Reconstructing the system coefficients for coupled harmonic oscillators” by Bartsch, J.; Barakat, A.A.; Buchwald, S.; Ciaramella, G.; Volkwein, S.; Weig, E.M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/105-2024.pdf Abstract: Physical models often contain unknown functions and relations. In order to gain more insights into the nature of physical processes, these unknown functions have to be identified or reconstructed. Mathematically, we can formulate this research question within the framework of inverse problems. In this work, we consider optimization techniques to solve the inverse problem using Tikhonov regularization and data from laboratory experiments. We propose an iterative strategy that eliminates the need for laboratory experiments. Our method is applied to identify the coupling and damping coefficients in a system of oscillators, ensuring an efficient and experiment-free approach. We present our results and compare them with those obtained from an alternative, purely experimental approach. By employing our proposed strategy, we demonstrate a significant reduction in the number of laboratory experiments required.
You may also like
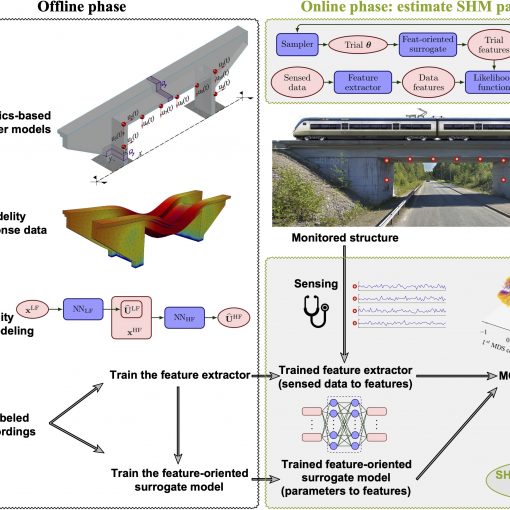
A new MOX Report entitled “Enhancing Bayesian model updating in structural health monitoring via learnable mappings” by Torzoni, M.; Manzoni, A.; Mariani, […]
A new MOX Report entitled “The lifex library version 2.0” by Bucelli, M. has appeared in the MOX Report Collection. Check it […]
A new MOX Report entitled “Computationally efficient techniques for Spatial Regression with Differential Regularization” by Arnone, E.; De Falco, C.; Formaggia, L.; […]
A new MOX Report entitled “Nonlinear morphoelastic theory of biological shallow shells with initial stress” by Andrini, D.; Magri, M.; Ciarletta, P. […]