A new MOX Report entitled “Real-time optimal control of high-dimensional parametrized systems by deep-learning based reduced order models” by Tomasetto, M.; Manzoni, A.; Braghin, F. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/43-2025.pdf
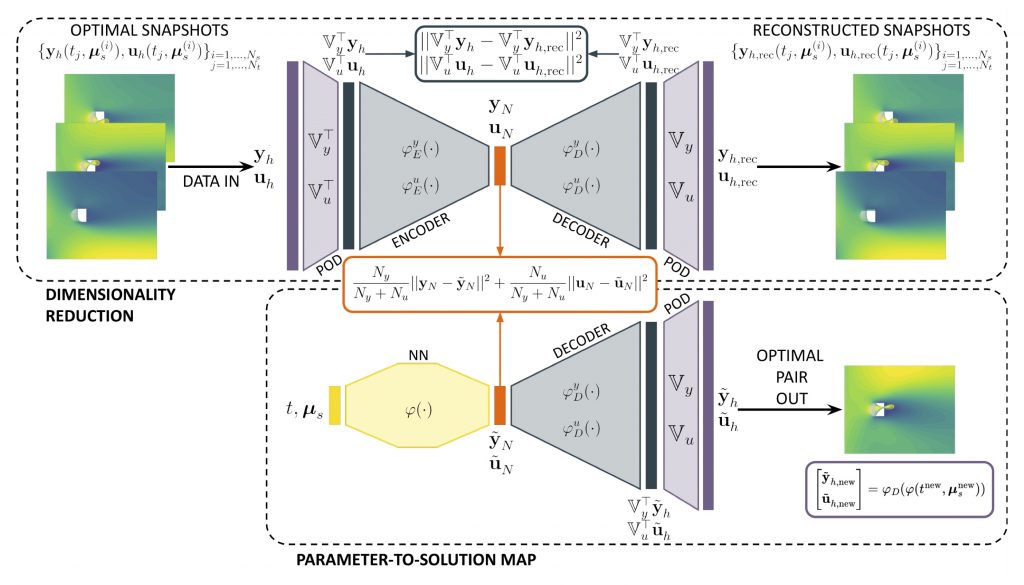
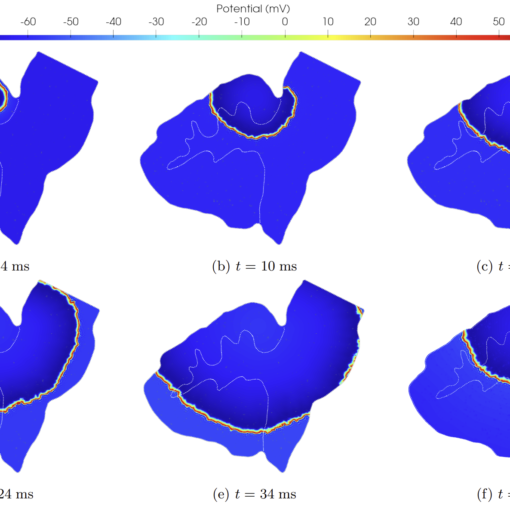
Abstract: Steering a system towards a desired target in a very short amount of time is a challenging task from a computational standpoint. Indeed, the intrinsically iterative nature of optimal control problems requires multiple simulations of the state of the physical system to be controlled. Moreover, the control action needs to be updated whenever the underlying scenario undergoes variations, as it often happens in applications. Full-order models based on, e.g., the Finite Element Method, do not meet these requirements due to the computational burden they usually entail. On the other hand, conventional reduced order modeling techniques such as the Reduced Basis method, despite their rigorous construction, are intrusive, rely on a linear superimposition of modes, and lack of efficiency when addressing nonlinear time-dependent dynamics. In this work, we propose a non-intrusive Deep Learning-based Reduced Order Modeling (DL-ROM) technique for the r! apid cont rol of systems described in terms of parametrized PDEs in multiple scenarios. In particular, optimal full-order snapshots are generated and properly reduced by either Proper Orthogonal Decomposition or deep autoencoders (or a combination thereof) while feedforward neural networks are exploited to learn the map from scenario parameters to reduced optimal solutions. Nonlinear dimensionality reduction therefore allows us to consider state variables and control actions that are both low-dimensional and distributed. After (i) data generation, (ii) dimensionality reduction, and (iii) neural networks training in the offline phase, optimal control strategies can be rapidly retrieved in an online phase for any scenario of interest. The computational speedup and the extremely high accuracy obtained with the proposed approach are finally assessed on different PDE-constrained optimization problems, ranging from the minimization of energy dissipation in incompressible flows modeled thro! ugh Navie r-Stokes equations to the thermal active cooling in heat transfer.