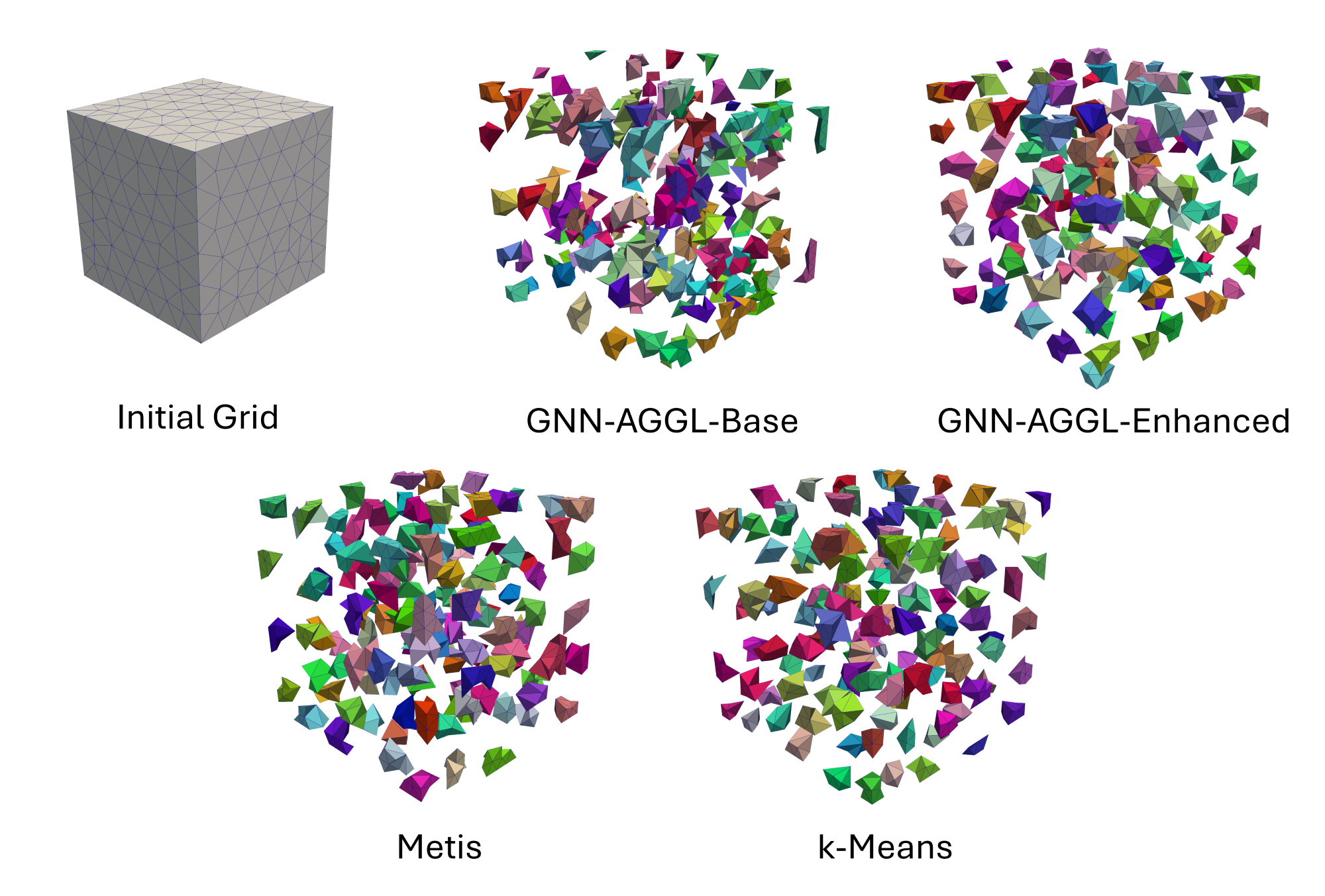
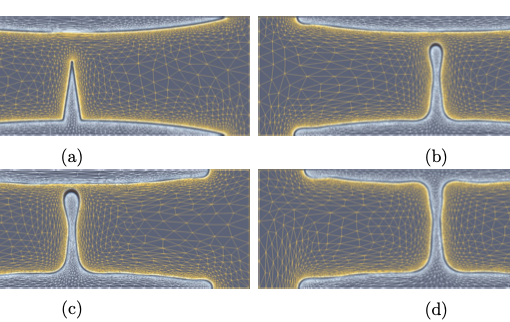
A new MOX Report entitled “Polytopal mesh agglomeration via geometrical deep learning for three-dimensional heterogeneous domains” by Antonietti, P.F.; Corti, M., Martinelli, G. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/43-2024.pdf Abstract: Agglomeration techniques are important to reduce the computational costs of numerical simulations and stand at the basis of multilevel algebraic solvers. To automatically perform the agglomeration of polyhedral grids, we propose a novel Geometrical Deep Learning-based algorithm that can exploit the geometrical and physical information of the underlying computational domain to construct the agglomerated grid and simultaneously guarantee the agglomerated grid’s quality. In particular, we propose a bisection model based on Graph Neural Networks (GNNs) to partition a suitable connectivity graph of computational three-dimensional meshes. The new approach has a high online inference speed and can simultaneously process the graph structure of the mesh, the geometrical information of the mesh (e.g. elements’ volumes, centers’ coordinates), and the physical information of the domain (e.g. physical parameters). Taking advantage of this new approach, our al! gorithm c an agglomerate meshes of a domain composed of heterogeneous media in an automatic way. The proposed GNN techniques are compared with the k-means algorithm and METIS: standard approaches for graph partitioning that are meant to process only the connectivity information on the mesh. We demonstrate that the performance of our algorithms outperforms available approaches in terms of quality metrics and runtimes. Moreover, we demonstrate that our algorithm also shows a good level of generalization when applied to more complex geometries, such as three-dimensional geometries reconstructed from medical images. Finally, the capabilities of the model in performing agglomeration of heterogeneous domains are tested in the framework of problems containing microstructures and on a complex geometry such as the human brain.
