A new MOX Report entitled “On latent dynamics learning in nonlinear reduced order modeling” by Farenga, N.; Fresca, S.; Brivio, S.; Manzoni, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/100-2024.pdf Abstract: In this work, we present the novel mathematical framework of latent dynamics models (LDMs) for reduced order modeling of parameterized nonlinear time-dependent PDEs. Our framework casts this latter task as a nonlinear dimensionality reduction problem, while constraining the latent state to evolve accordingly to an (unknown) dynamical system, namely a latent vector ordinary differential equation (ODE). A time-continuous setting is employed to derive error and stability estimates for the LDM approximation of the full order model (FOM) solution. We analyze the impact of using an explicit Runge-Kutta scheme in the time-discrete setting, and further explore the learnable setting where deep neural networks approximate the discrete LDM components, while providing a bounded approximation error with respect to the FOM. Moreover, we extend the concept of parameterized Neural ODE – recently proposed as a possible way to build data-driven dynamical systems w! ith varyi ng input parameters – to be a convolutional architecture, where the input parameters information is injected by means of an affine modulation mechanism, while designing a convolutional autoencoder neural network able to retain spatial-coherence, thus enhancing interpretability at the latent level. Numerical experiments, including the Burgers’ and the advection-reaction-diffusion equations, demonstrate the framework’s ability to obtain, in a multi-query context, a time-continuous approximation of the FOM solution, thus being able to query the LDM approximation at any given time instance while retaining a prescribed level of accuracy. Our findings highlight the remarkable potential of the proposed LDMs, representing a mathematically rigorous framework to enhance the accuracy and approximation capabilities of reduced order modeling for time-dependent parameterized PDEs.
You may also like
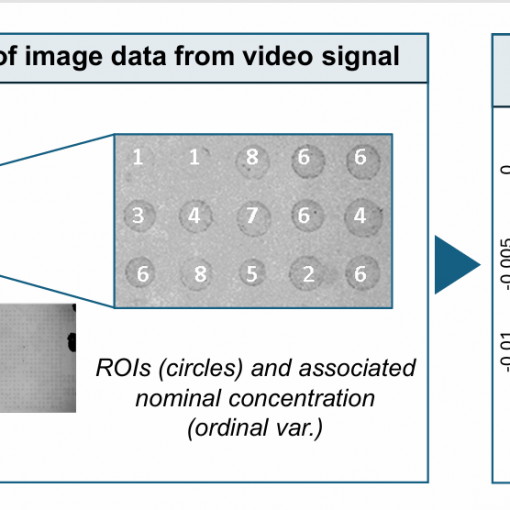
A new MOX Report entitled “Functional-Ordinal Canonical Correlation Analysis With Application to Data from Optical Sensors” by Patanè, G.; Nicolussi, F.; Krauth, […]
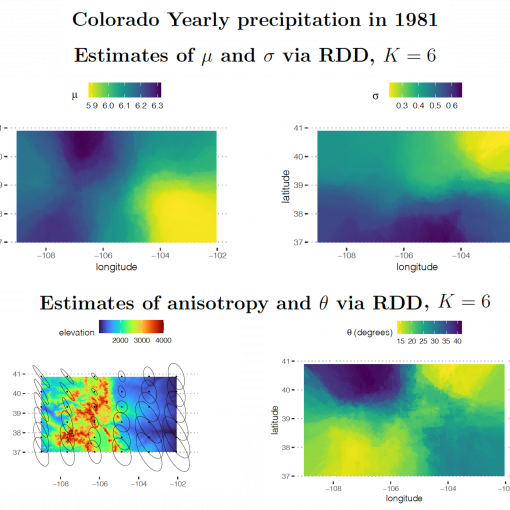
A new MOX Report entitled “Estimating Non-Stationarity in Spatial Processes: an approach based on Random Domain Decomposition” by Scimone, R.; Menafoglio, A.; […]
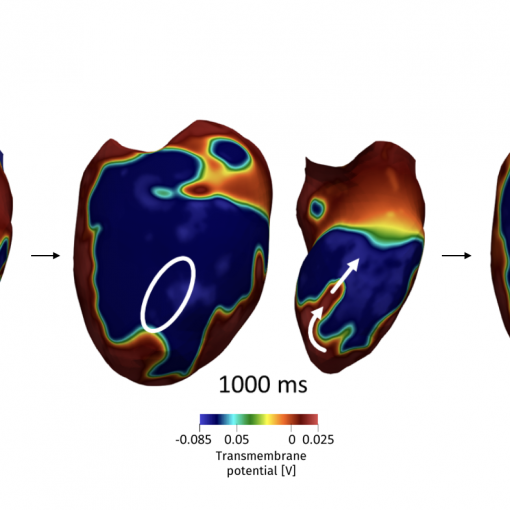
A new MOX Report entitled “Influence of patient-specific acute myocardial ischemia maps on arrhythmogenesis: a computational study” by Corda, A.; Pagani, S.; […]
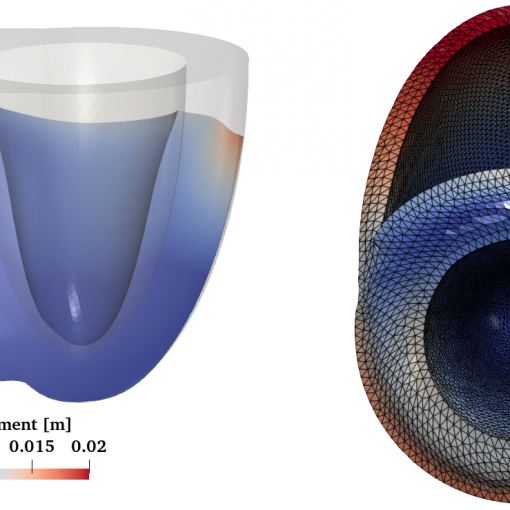
A new MOX Report entitled “A software benchmark for cardiac elastodynamics” by Arostica, R.; Nolte, D.; Brown, A.; Gebauer, A.; Karabelas, E.; […]