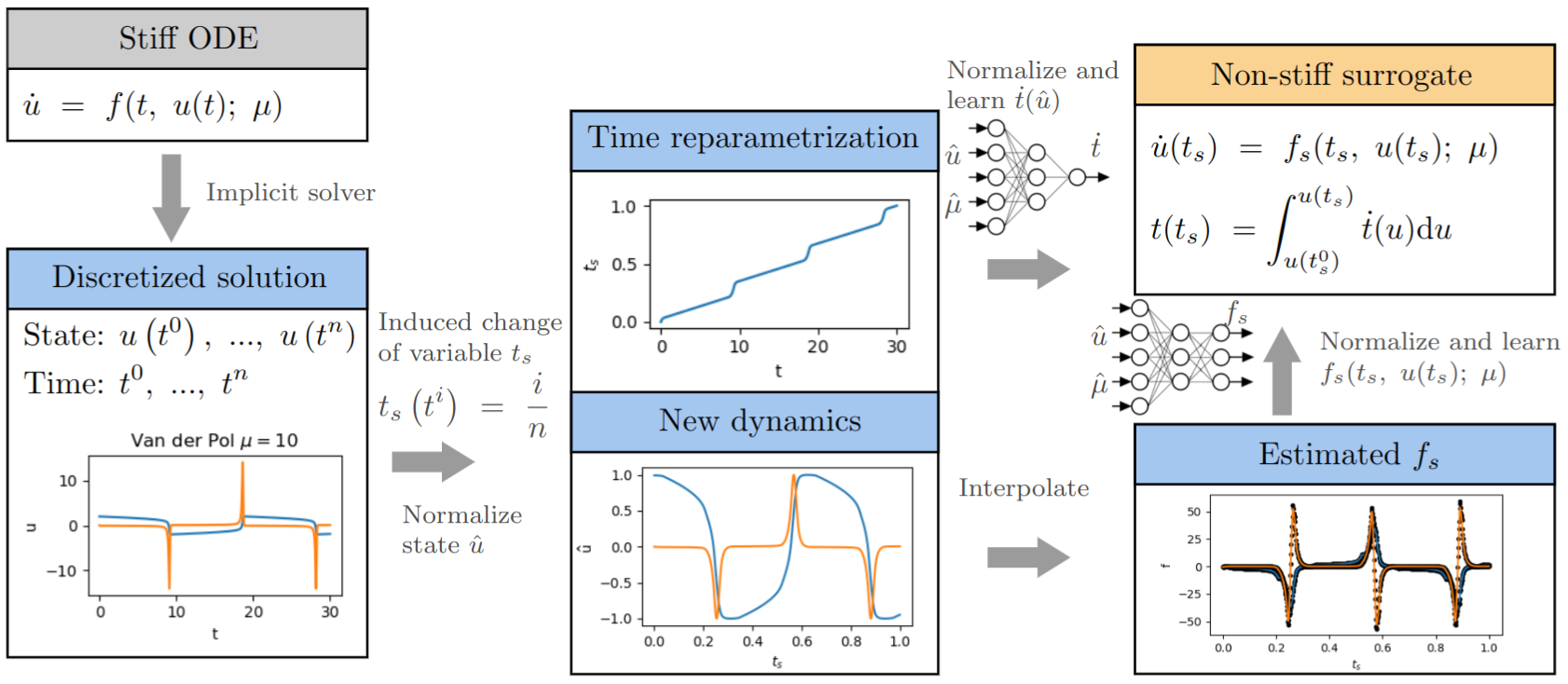
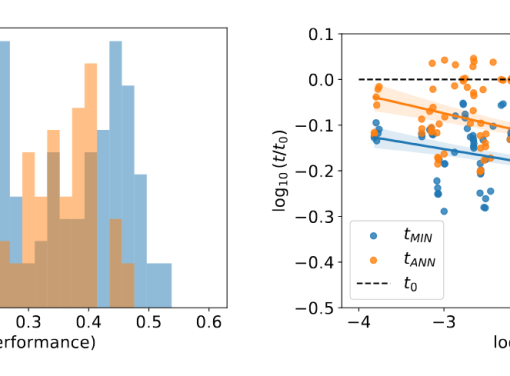
A new MOX Report entitled “Neural ordinary differential equations for model order reduction of stiff systems” by Caldana, M.; Hesthaven, J. S. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/53-2024.pdf Abstract: Neural Ordinary Differential Equations (ODEs) represent a significant advancement at the intersection of machine learning and dynamical systems, offering a continuous-time analog to discrete neural networks. Despite their promise, deploying neural ODEs in practical applications often encounters the challenge of stiffness, a condition where rapid variations in some components of the solution demand prohibitively small time steps for explicit solvers. This work addresses the stiffness issue when employing neural ODEs for model order reduction by introducing a suitable reparametrization in time. The considered map is data-driven and it is induced by the adaptive time-stepping of an implicit solver on a reference solution. We show the map produces a nonstiff system that can be cheaply solved with an explicit time integration scheme. The original, stiff, time dynamic is recovered by means of a map learnt by a neural network that connects the state spa! ce to the time reparametrization. We validate our method through extensive experiments, demonstrating improvements in efficiency for the neural ODE inference while maintaining robustness and accuracy. The neural network model also showcases good generalization properties for times beyond the training data.
