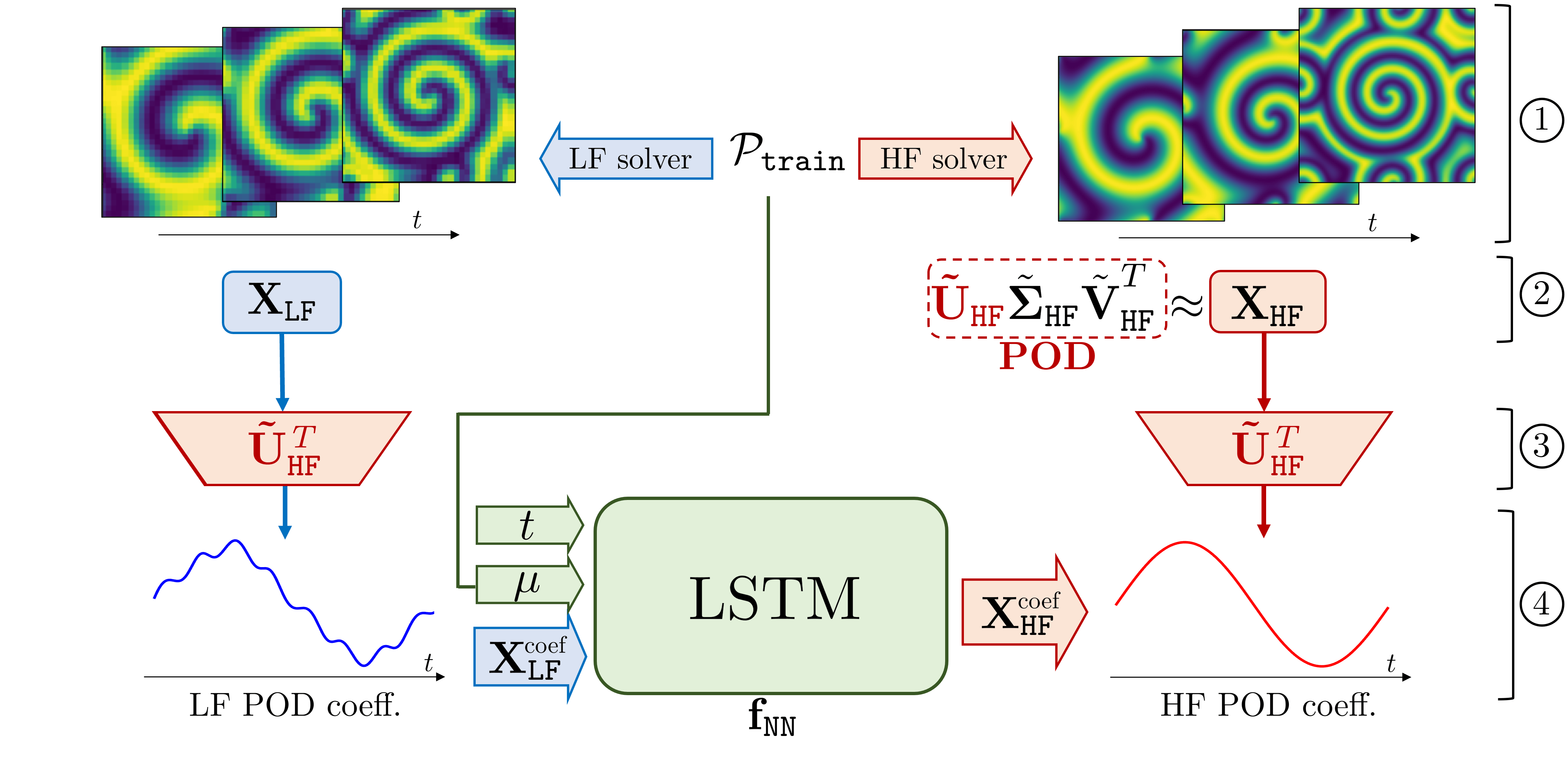
A new MOX Report entitled “Multi-fidelity reduced-order surrogate modelling” by Conti, P.; Guo, M.; Manzoni, A.; Frangi, A.; Brunton, S. L.; Kutz, J.N. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/83-2024.pdf Abstract: High-fidelity numerical simulations of partial differential equations (PDEs) given a restricted computational budget can significantly limit the number of parameter configurations considered and/or time window evaluated. Multi-fidelity surrogate modelling aims to leverage less accurate, lower-fidelity models that are computationally inexpensive in order to enhance predictive accuracy when high-fidelity data are scarce. However, low-fidelity models, while often displaying the qualitative solution behaviour, fail to accurately capture fine spatio temporal and dynamic features of high-fidelity models. To address this shortcoming, we present a data-driven strategy that combines dimensionality reduction with multi-fidelity neural network surrogates. The key idea is to generate a spatial basis by applying proper orthogonal decomposition (POD) to high-fidelity solution snapshots, and approximate the dynamics of the reduced states – time-parameter-depend! ent expan sion coefficients of the POD basis – using a multi-fidelity long short-term memory network. By mapping low-fidelity reduced states to their high-fidelity counterpart, the proposed reduced-order surrogate model enables the efficient recovery of full solution fields over time and parameter variations in a non-intrusive manner. The generality of this method is demonstrated by a collection of PDE problems where the low-fidelity model can be defined by coarser meshes and/or time stepping, as well as by misspecified physical features.
You may also like
A new MOX Report entitled “Reconstruction of unknown nonlienar operators in semilinear elliptic models using optimal inputs” by Bartsch, J.; Buchwald, S.; […]
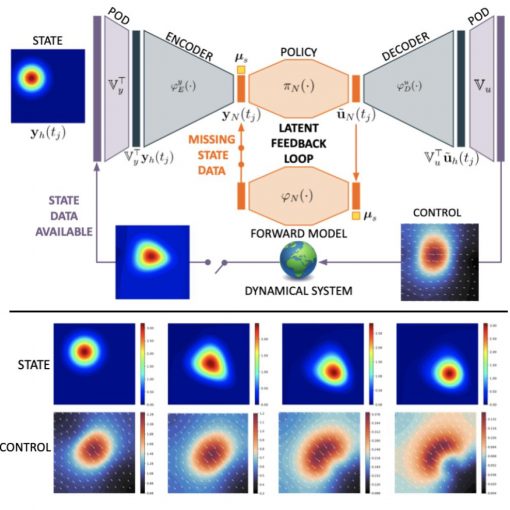
A new MOX Report entitled “Latent feedback control of distributed systems in multiple scenarios through deep learning-based reduced order models ” by […]
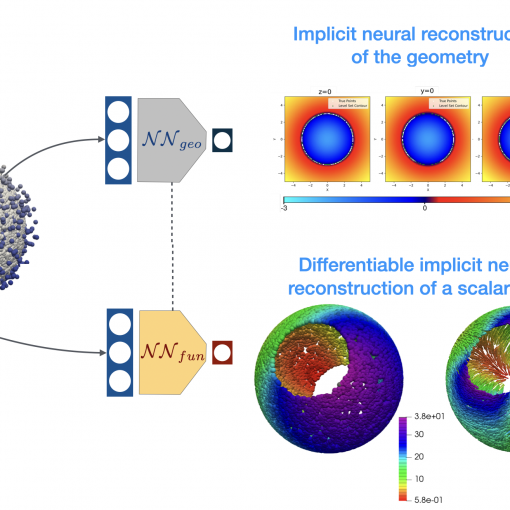
A new MOX Report entitled “Implicit neural field reconstruction on complex shapes from scattered and noisy data” by Carrara, D.; Regazzoni, F.; […]
A new MOX Report entitled “The lifex library version 2.0” by Bucelli, M. has appeared in the MOX Report Collection. Check it […]