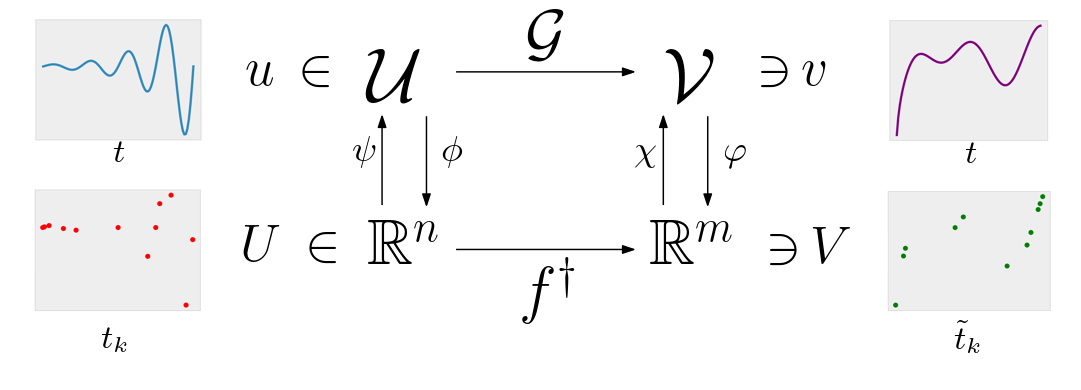A new MOX Report entitled “Learning epidemic trajectories through Kernel Operator Learning: from modelling to optimal control” by Ziarelli, G.; Parolini, N.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/32-2024.pdf Abstract: Since infectious pathogens start spreading into a susceptible population, mathematical models can provide policy makers with reliable forecasts and scenario analyses, which can be concretely implemented or solely consulted. In these complex epidemiological scenarios, machine learning architectures can play an important role, since they directly reconstruct data-driven models circumventing the specific modelling choices and the parameter calibration, typical of classical compartmental models. In this work, we discuss the efficacy of Kernel Operator Learning (KOL) to reconstruct population dynamics during epidemic outbreaks, where the transmission rate is ruled by an input strategy. In particular, we introduce two surrogate models, named KOL-m and KOL-$\partial$, which reconstruct in two different ways the evolution of the epidemics. Moreover, we evaluate the generalization performances of the two approaches with different kernels, including the Ne! ural Tang ent Kernels, and compare them with a classical neural network model learning method. Employing synthetic but semi-realistic data, we show how the two introduced approaches are suitable for realizing fast and robust forecasts and scenario analyses, and how these approaches are competitive for determining optimal intervention strategies with respect to specific performance measures.
