A new MOX Report entitled ” Improvements on uncertainty quantification with variational autoencoders” by Tonini, A.; Bui-Thanh, T.; Regazzoni, F.; Dede’, L; Quarteroni, A. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/56-2025.pdf
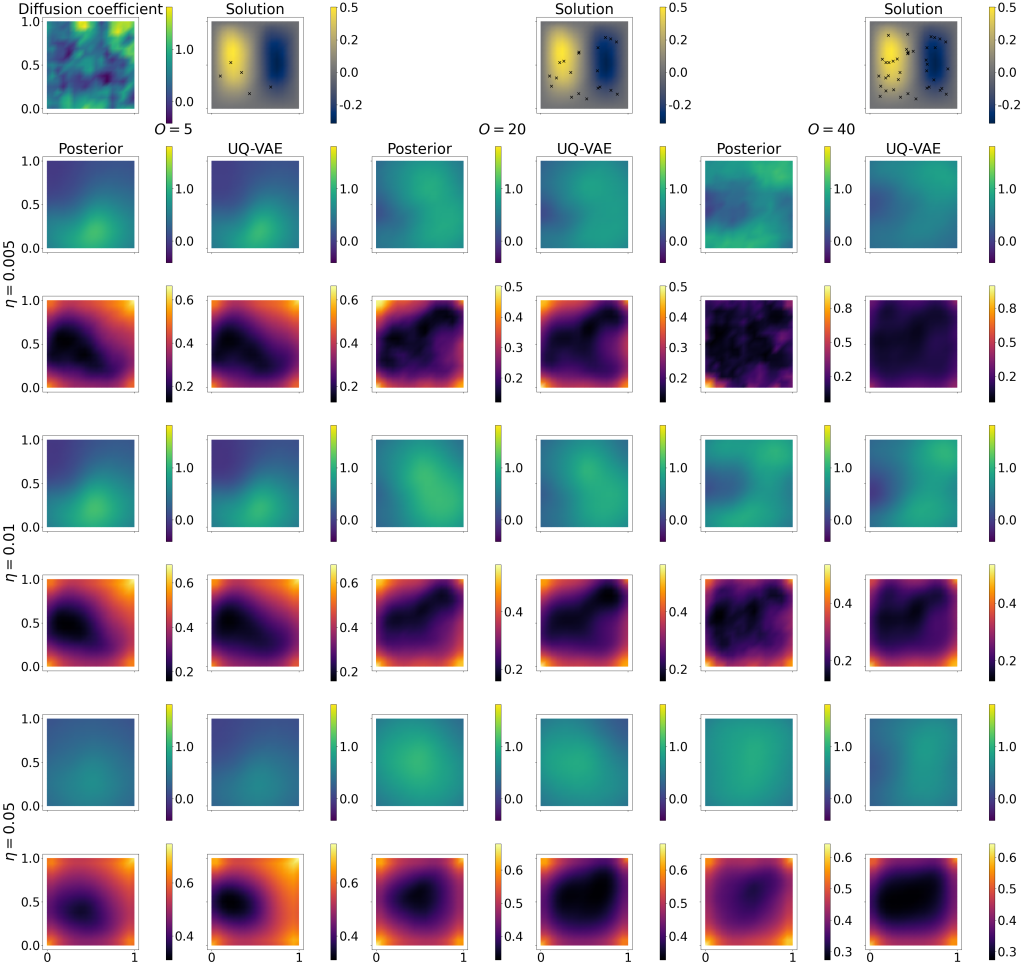
Abstract: Inverse problems aim to determine model parameters of a mathematical problem from given observational data. Neural networks can provide an efficient tool to solve these problems. In the context of Bayesian inverse problems, Uncertainty Quantification Variational AutoEncoders (UQ-VAE), a class of neural networks, approximate the posterior distribution mean and covariance of model parameters. This allows for both the estimation of the parameters and their uncertainty in relation to the observational data. In this work, we propose a novel loss function for training UQ-VAEs, which includes, among other modifications, the removal of a sample mean term from an already existing one. This modification improves the accuracy of UQ-VAEs, as the original theoretical result relies on the convergence of the sample mean to the expected value (a condition that, in high dimensional parameter spaces, requires a prohibitively large number of samples due to! the curs e of dimensionality). Avoiding the computation of the sample mean significantly reduces the training time in high dimensional parameter spaces compared to previous literature results. Under this new formulation, we establish a new theoretical result for the approximation of the posterior mean and covariance for general mathematical problems. We validate the effectiveness of UQ-VAEs through three benchmark numerical tests: a Poisson inverse problem, a non affine inverse problem and a 0D cardiocirculatory model, under the two clinical scenarios of systemic hypertension and ventricular septal defect. For the latter case, we perform forward uncertainty quantification.