A new MOX Report entitled “Deep orthogonal decomposition: a continuously adaptive neural network approach to model order reduction of parametrized partial differential equations” by Franco, N. R.; Manzoni, A.; Zunino, P.; Hesthaven, J. S. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/42-2025.pdf
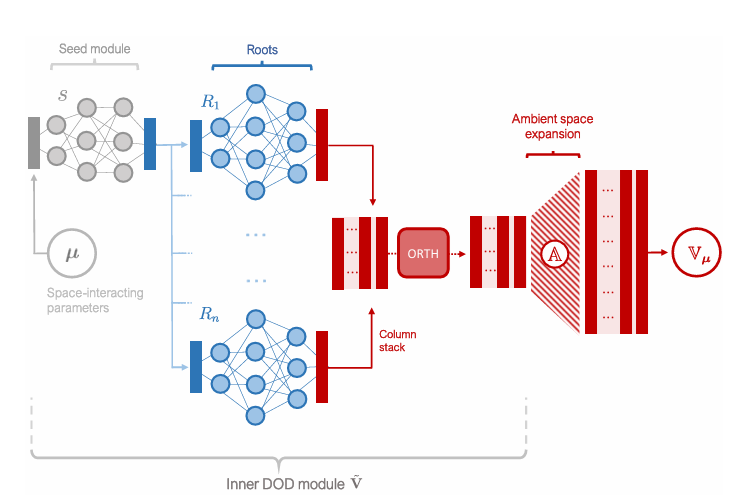
Abstract: Wedevelop a novel deep learning technique, termed Deep Orthogonal Decomposition (DOD), for dimensionality reduction and reduced order modeling of parameter dependent partial differential equations. The approach involves constructing a deep neural network model that approximates the solution manifold using a continuously adaptive local basis. In contrast to global methods, such as Principal Orthogonal Decomposition (POD), this adaptivity allows the DODtomitigate the Kolmogorov barrier when dealing with space-interacting parameters, making the approach applicable to a wide spectrum of parametric problems. Leveraging this idea, we use the DOD to construct an adaptive alternative to the so-called POD-NN method, here termed DOD-NN. The approach is fully data-driven and nonintrusive but, at the same time, allows for a tight control on error propagation and remains highly interpretable thanks to the rich structure present in the latent space. For this reason, the proposed approach stands out as a valuable alternative to other nonlinear model order reduction techniques, such as those based on deep autoencoders. The methodology is discussed both theoretically and practically, evaluating its performances on problems involving nonlinear PDEs, parametrized geometries and high-dimensional parameter spaces. Finally, we conclude with a brief discussion on potential applications of the DOD beyond DOD-NN, featuring, for instance, the integration of our approach within intrusive reduced order models such as the Reduced Basis Method.