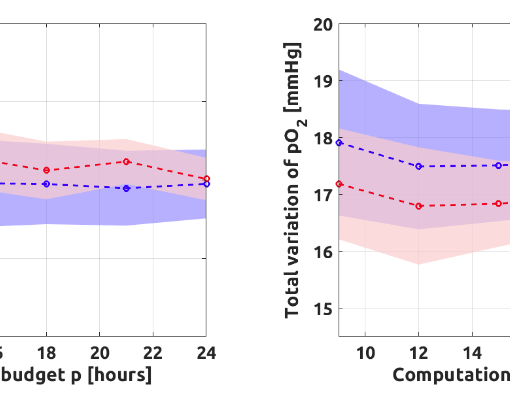
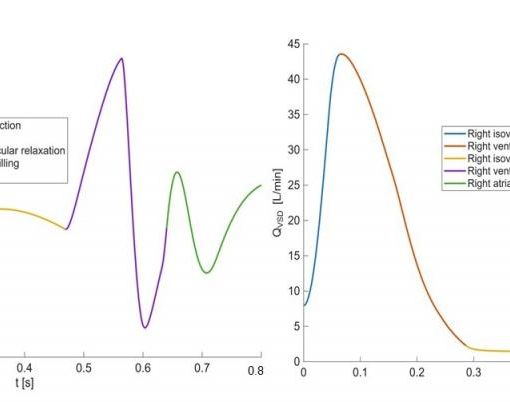
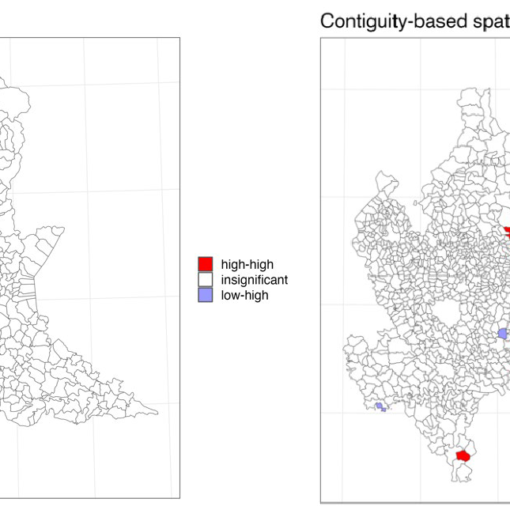
A new MOX Report entitled “Deep Learning-based surrogate models for parametrized PDEs: handling geometric variability through graph neural networks” by Franco, N.R.; Fresca, S.; Tombari, F.; Manzoni, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/94-2024.pdf Abstract: Mesh-based simulations play a key role when modeling complex physical systems that, in many disciplines across science and engineering, require the solution of parametrized time-dependent nonlinear partial differential equations (PDEs). In this context, full order models (FOMs), such as those relying on the finite element method, can reach high levels of accuracy, however often yielding intensive simulations to run. For this reason, surrogate models are developed to replace computationally expensive solvers with more efficient ones, which can strike favorable trade-offs between accuracy and efficiency. This work explores the potential usage of graph neural networks (GNNs) for the simulation of time-dependent PDEs in the presence of geometrical variability. In particular, we propose a systematic strategy to build surrogate models based on a data-driven time-stepping scheme where a GNN architecture is used to efficiently evolve the system. With res! pect to t he majority of surrogate models, the proposed approach stands out for its ability of tackling problems with parameter dependent spatial domains, while simultaneously generalizing to different geometries and mesh resolutions. We assess the effectiveness of the proposed approach through a series of numerical experiments, involving both two- and three-dimensional problems, showing that GNNs can provide a valid alternative to traditional surrogate models in terms of computational efficiency and generalization to new scenarios. We also assess, from a numerical standpoint, the importance of using GNNs, rather than classical dense deep neural networks, for the proposed framework.
[attach 1]