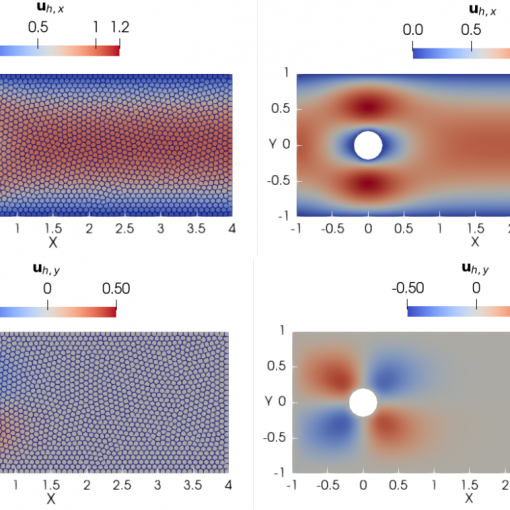
A new MOX Report entitled “A geometry aware arbitrary order collocation Boundary Element Method solver for the potential flow past three dimensional lifting surfaces” by Cattarossi, L.; Sacco, F.; Giuliani, N.; Parolini, N.; Mola, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/75-2024.pdf Abstract: This work presents a numerical model for the simulation of potential flow past three dimensional lifting surfaces. The solver is based on the collocation Boundary Element Method, combined with Galerkin variational formulation of the nonlinear Kutta condition imposed at the trailing edge. A similar Galerkin variational formulation is also used for the computation of the fluid velocity at the wake collocation points, required by the relaxation algorithm which aligns the wake with the local flow. The use of such a technique, typically associated with the Finite Element Method, allows in fact for the evaluation of the solution derivatives in a way that is independent of the local grid topology. As a result of this choice, combined with the direct interface with CAD surfaces, the solver is able to use arbitrary order Lagrangian elements on automatically refined grids. Numerical results on a rectangular wing with NACA 0012 airfoil sections are presente! d to comp are the accuracy improvements obtained by grid spatial refinement or by discretization degree increase. Finally, numerical results on rectangular and swept wings with NACA 0012 airfoil section confirm that the model is able to reproduce experimental data with good accuracy.
You may also like
A new MOX Report entitled “Joint modelling of recurrent and terminal events with discretely-distributed non-parametric frailty: application on re-hospitalizations and death in […]
A new MOX Report entitled “Two new calibration techniques of lumped-parameter mathematical models for the cardiovascular system” by Tonini, A., Regazzoni, F., […]
A new MOX Report entitled “A polytopal discontinuous Galerkin method for the pseudo-stress formulation of the unsteady Stokes problem” by Antonietti, P.F.; […]
A new MOX Report entitled “A mixed-dimensional formulation for the simulation of slender structures immersed in an incompressible flow” by Lespagnol, F.; […]