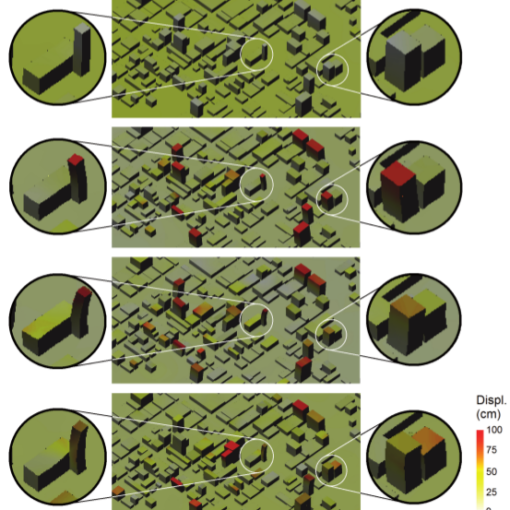
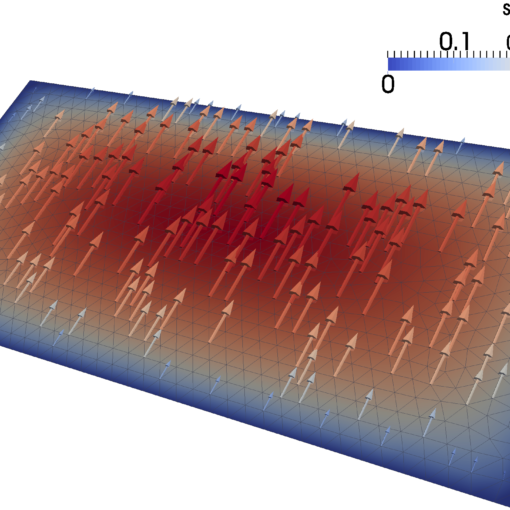
Subsurface flows are strongly influenced by the presence of fractures. While small and micro-fractures can be easily accounted for by means of upscaling techniques, large fractures and faults play a more complex role, acting as paths or barriers for the flow. These effects are very relevant for many applications such as oil migration, oil recovery, CO2 storage and groundwater contamination and remediation. The typical size of these features, compared to the domain size, is usually such that a very fine mesh is needed to resolve the fracture width. Moreover, in realistic cases, the porous media are usually crossed by a large number of fractures that can intersect each other. If we consider the finite element method on an unstructured tetrahedral grid the construction of a good computational grid is essential to achieve accurate
results. However, the conformity of the grid to possibly numerous and intersecting fractures can be a strong constraint and can affect the quality of the elements. Besides, the mesh refinement required to capture the faults or fractures aperture leads to a very high, if not unaffordable, computational cost.
We consider a method to remove the constraint of mesh conformity by means of the extended finite element method (XFEM), allowing the fracture to cross the elements of the grid in an arbitrary way. The XFEM are widely used in the simulation of the mechanics of fractured media, while their application to flow problems in the presence of fractures and heterogeneities is still at the beginning. This approach has reduced the effort in constructing the computational grid, since this operation does not have to account for the possibly complicated geometry of the fractures and, moreover, can be performed only once even if the position of fractures or faults changes due to multiple scenarios or sensitivity analysis.
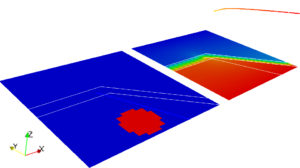
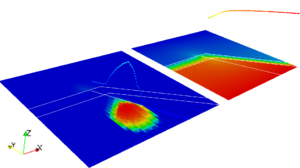
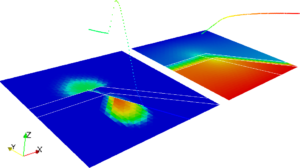
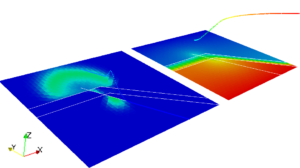
In each of the four images are reported the wetting phase saturation, in the bottom-left part, and global pressure, in the top-right part. Each figure report the solutions at different times, from left to right and from top to bottom. The fractures propagates with an imposed time law cutting the impermeable layer.
The accurate modeling of flow through complex networks of thousands of intersecting fractures in a reservoir is important for many types of problems related to the oil industry. The Discrete Fracture Model (DFM) represents one of the most accurate methodologies for accurately describing flow in fracture networks as it entails the direct numerical simulation of flow through the fractured porous media. Using DFM, the rock matrix and fractures are represented explicitly and Darcy flow equations are solved. However, one of the major drawbacks of this method is the high computational cost.
A numerical upscaling technique based on the numerical solution of the fracture network and matrix flow at a local fine scale is preferable. We have developed an accurate representation of fracture networks to obtain an upscaled representation of the porous medium system through the use of a multiple sub-region technique. We have addressed the 3D problem directly and considered corner-point grids, typically met in reservoir simulations. The object was to enable the computation of flow in the upscaled grid (at reservoir scale) by the computation of appropriate transmissibility between fracture and matrix, among fractures, and among different matrix blocks.
Oil saturation inside the fractures. Initially the fractures are full of oil, then, as the injector well pumps in the oil, the water saturation increases and the production well extracts oil.
