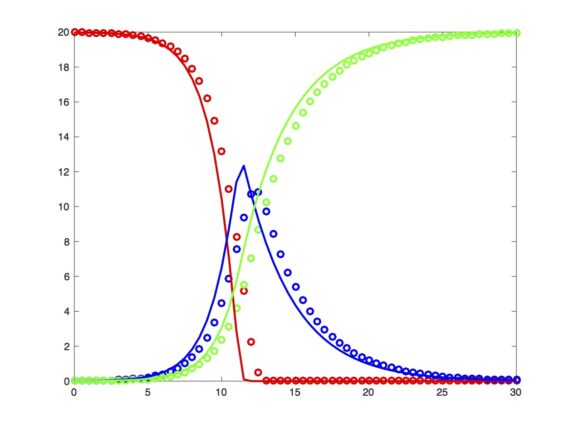
An open-access journal paper entitled “A mathematical dashboard for the analysis of Italian COVID-19 epidemic data” by Nicola Parolini, Giovanni Ardenghi, Luca Dede’ and Alfio Quarteroni has been published in Numerical Methods in Biomedical Engineering. The paper proposes an analysis of the COVID-19 epidemic on the basis of the epiMOX dashboard […]
Nicola Parolini
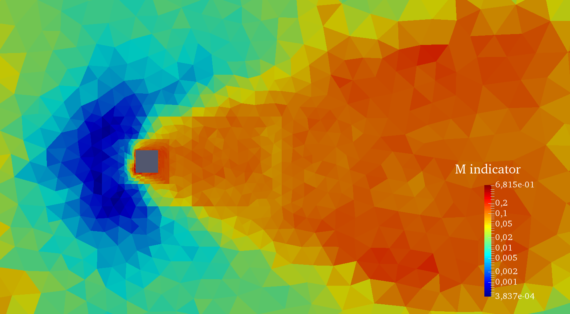
A new MOX report entitled “An efficient and accurate implicit DG solver for the incompressible Navier-Stokes equations” by Giuseppe Orlando, Alessandro Della Rocca, Paolo Barbante, Luca Bonaventura and Nicola Parolini has appeared in the MOX Report Collection. The report can be donwloaded at the following link: https://www.mate.polimi.it/biblioteca/add/qmox/47-2021.pdf Abstract: We […]
L’infettivologo Matteo Bassetti e il matematico Alfio Quarteroni discutono su come comunicare la pandemia di Covid19 affinché la campagna vaccinale, le regole e, quando necessarie, le restrizioni vengano comprese come l’unica strada possibile verso il superamento della pandemia. “Festival del libro possibile”, Polignano a Mare, 8 luglio 2021.
From August 16 to 30, 2021 the MOX Laboratory will be the featured node on the website of the European Consortium for Mathematics in Industry (ECMI). ECMI is a consortium of academic institutions and industrial companies that promote and support the use of mathematical modelling, simulation, and optimization in any […]
Un’intervista ad Alfio Quarteroni sulla necessità di una buona comprensione matematica dei dati.
Since 2016, MOX is collaborating with a leading tire manufacturing company for the development of reduced model for the analysis and prediction of the mixing process in continuous mixing facilities. A new project has been defined to further implement the numerical model and perform a complete assessment of the approach […]
Antonella Abbà, Luca Bonaventura and other group members published a paper in JCP presenting the first application of dynamic models in a VMS-DG framework. The paper can be downloaded here https://www.sciencedirect.com/science/article/pii/S0045793015002972
Former group member Alessandro Della Rocca of TENOVA RD and Luca Bonaventura published a paper in Journal of Scientific Computing on monotonic extensions of efficient second order stiff ODE solvers. The paper can be downloaded here https://link.springer.com/article/10.1007/s10915-016-0267-9
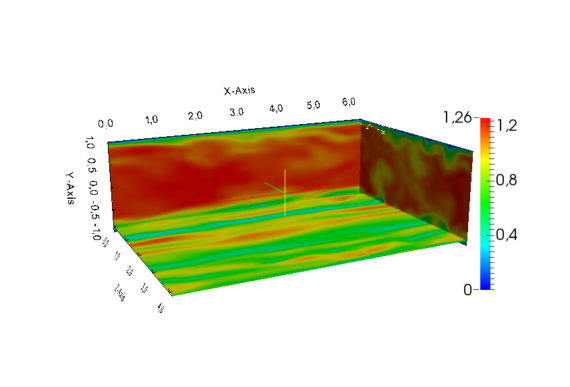
A paper on a p-adaptive approach to LES modelling of compressible flows with DG methods has been published by Antonella Abbà, Luca Bonaventura and other collaborators has been published in Journal of Computational Physics. The paper can be downloaded here https://www.sciencedirect.com/science/article/pii/S0021999117305788
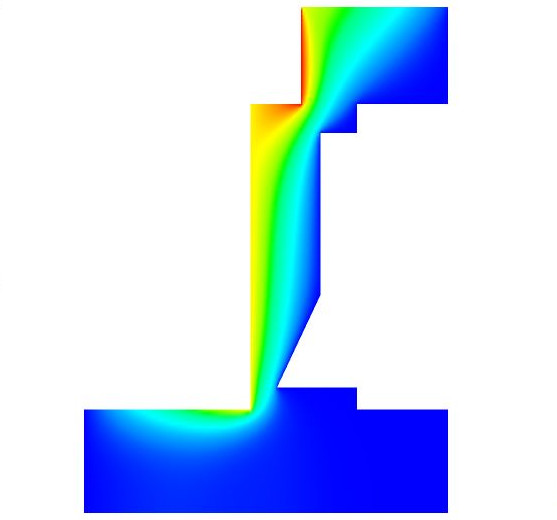
A new article on free-surface problems with moving contact line by Ivan Fumagalli, Nicola Parolini and Marco Verani has appeared on Journal of Computational Physics. The article can be downloaded at the following link https://authors.elsevier.com/a/1WD4K508Haf6U Title: On a free-surface problem with moving contact line: From variational principles to stable numerical approximations Authors: […]