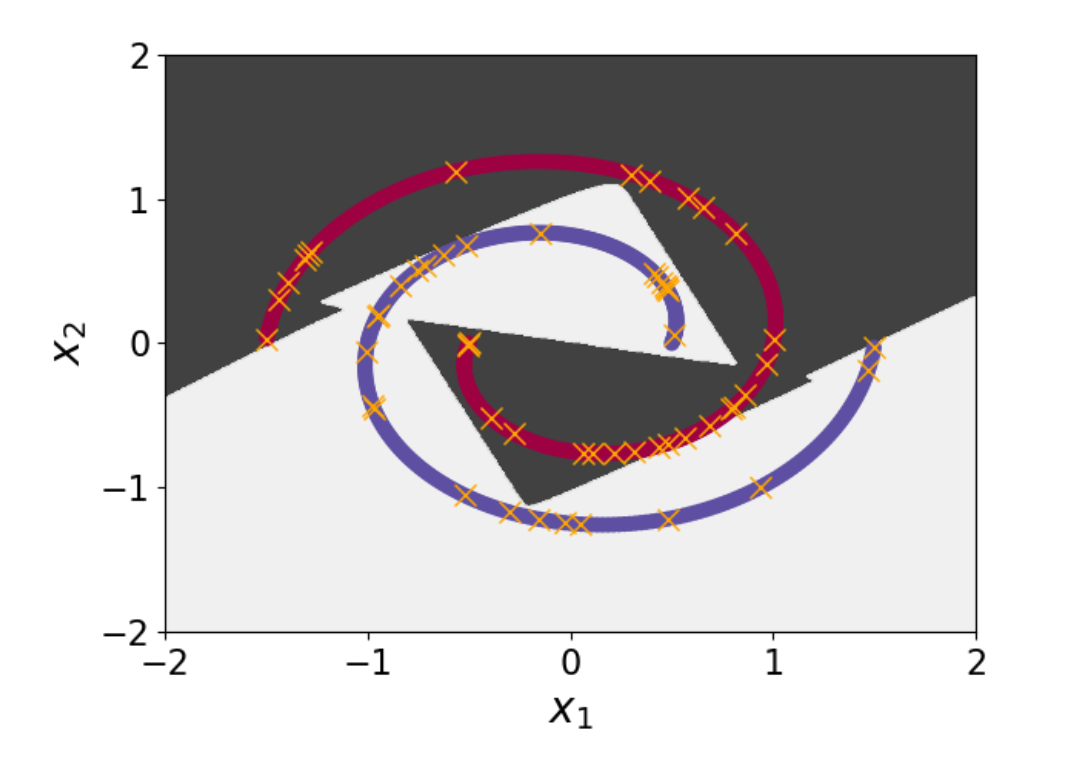
A new MOX Report entitled “Greedy reconstruction algorithms for function approximation” by Buchwald, S.; Ciaramella, G.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/05-2025.pdf Abstract: Two key elements in any function approximation problem are the selection of data points and the choice of the structure of the ansatz within a given family of approximation functions. This paper is devoted to the development and analysis of greedy reconstruction algorithms that address both aspects to improve approximation accuracy and efficiency. The general idea of these methods is to select an optimal set of data points while simultaneously identifying a minimal structure that is able to accurately approximate the selected data. Theoretical and numerical studies on polynomial interpolation and function approximation by neural networks demonstrate the efficiency of the proposed algorithms.
