A new MOX Report entitled “Numerical Solution of linear drift-diffusion and pure drift equations on one-dimensional graphs” by Crippa, B.; Scotti, A.; Villa, A has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/80-2024.pdf Abstract: We propose numerical schemes for the approximate solution of problems defined on the edges of a one-dimensional graph. In particular, we consider linear transport and a drift-diffusion equations, and discretize them by extending Finite Volume schemes with upwind flux to domains presenting bifurcation nodes with an arbitrary number of incoming and outgoing edges, and implicit time discretization. We show that the discrete problems admit positive unique solutions, and we test the methods on the intricate geometry of an electrical treeing.
You may also like
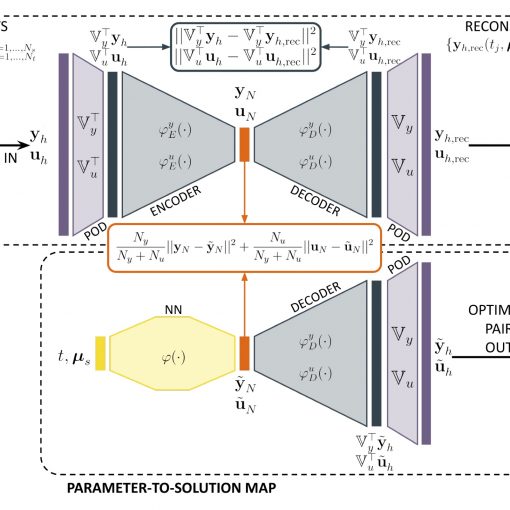
A new MOX Report entitled “Real-time optimal control of high-dimensional parametrized systems by deep-learning based reduced order models” by Tomasetto, M.; Manzoni, […]
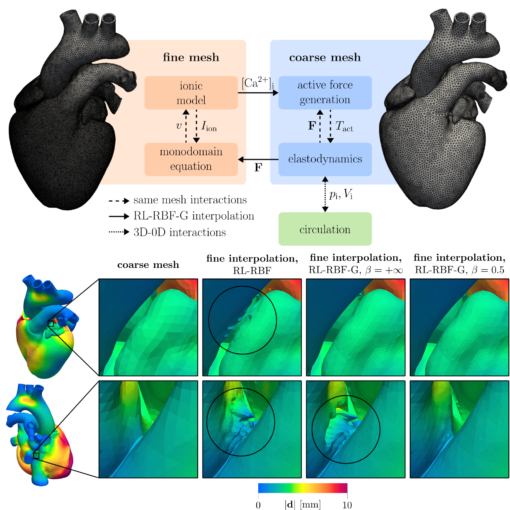
A new MOX Report entitled “Robust radial basis function interpolation based on geodesic distance for the numerical coupling of multiphysics problems” by […]
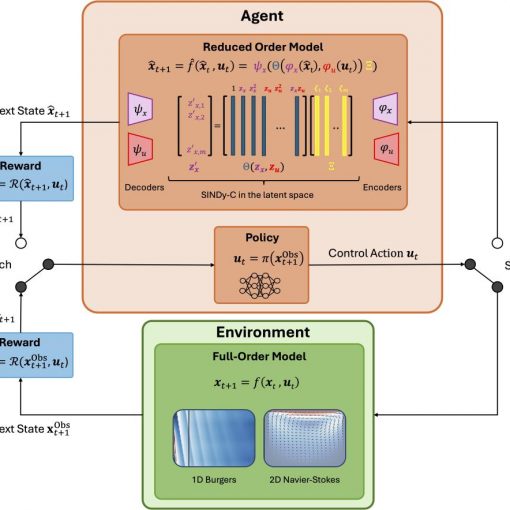
A new MOX Report entitled “Interpretable and efficient data-driven discovery and control of distributed systems” by Wolf, F.; Botteghi, N.; Fasel, U.; […]
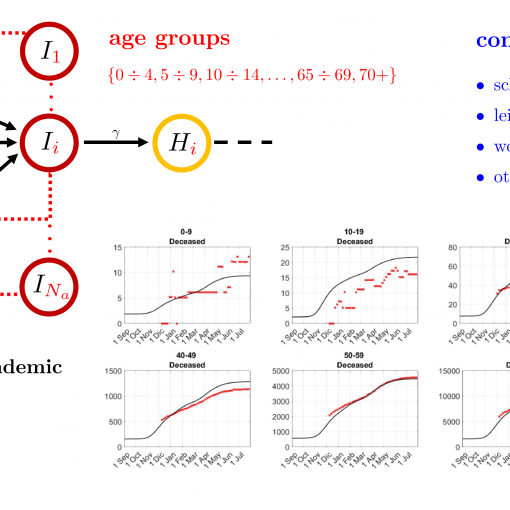
A new MOX Report entitled “SEIHRDV: a multi-age multi-group epidemiological model and its validation on the COVID-19 epidemics in Italy” by Dede’, […]