A new MOX Report entitled “A Necas-Lions inequality with symmetric gradients on star-shaped domains based on a first order Babuska-Aziz inequality” by Botti, M.; Mascotto, L. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/52-2024.pdf Abstract: We prove a Necas-Lions inequality with symmetric gradients on two and three dimensional domains that are star-shaped with respect to a ball B; the constants in the inequality are explicit with respect to the diameter and the radius of B. Crucial tools in deriving this inequality are a first order Babuska-Aziz inequality based on Bogovskii’s construction of a right-inverse of the divergence and Fourier transform techniques proposed by Duran. As a byproduct, we derive arbitrary order estimates in arbitrary dimension for that operator.
You may also like
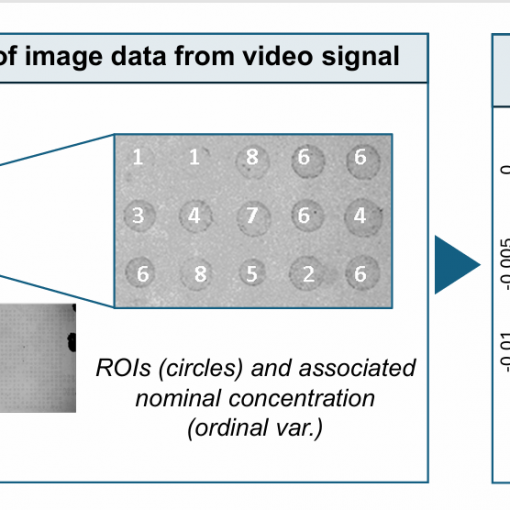
A new MOX Report entitled “Functional-Ordinal Canonical Correlation Analysis With Application to Data from Optical Sensors” by Patanè, G.; Nicolussi, F.; Krauth, […]
A new MOX Report entitled “Stability and interpolation estimates of Hellinger-Reissner virtual element spaces” by Botti, M.; Mascotto, L.; Vacca, G.; Visinoni, […]
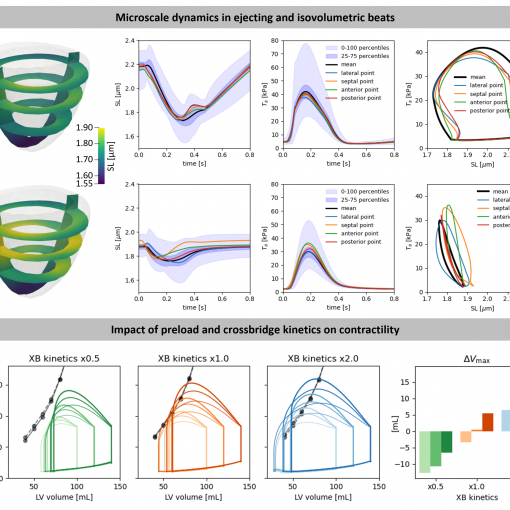
A new MOX Report entitled “Elucidating the cellular determinants of the end-systolic pressure-volume relationship of the heart via computational modelling” by Regazzoni, […]
A new MOX Report entitled “Numerical Solution of linear drift-diffusion and pure drift equations on one-dimensional graphs” by Crippa, B.; Scotti, A.; […]