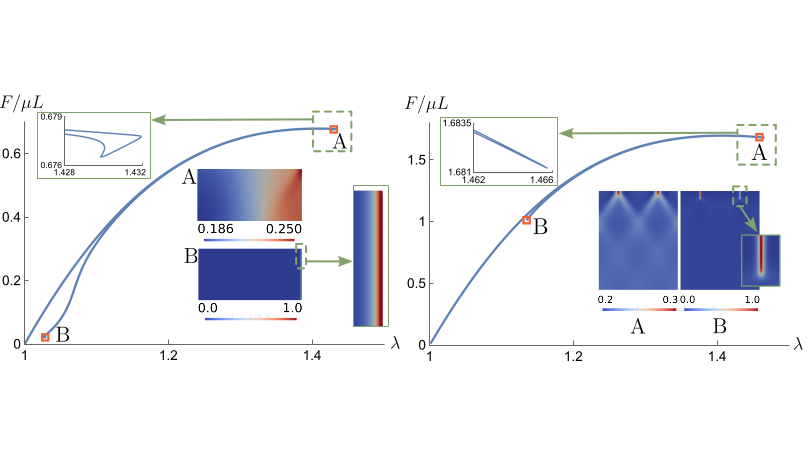
A new MOX Report entitled “Elastic Instability behind Brittle Fracture” by Riccobelli, D.; Ciarletta, P.; Vitale, G.; Maurini, C.; Truskinovsky, L. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/46-2024.pdf Abstract: We argue that nucleation of brittle cracks in initially flawless soft elastic solids is preceded by a nonlinear elastic instability, which cannot be captured without accounting for geometrical precise description of finite elastic deformation. As a prototypical problem we consider a homogeneous elastic body subjected to tension and assume that it is weakened by the presence of a free surface which then serves as a site of crack nucleation. We show that in this maximally simplified setting, brittle fracture emerges from a symmetry breaking elastic instability activated by softening and involving large elastic rotations. The implied bifurcation of the homogeneous elastic equilibrium is highly unconventional for nonlinear elasticity as it exhibits an extraordinary sensitivity to geometry, reminiscent of the transition to turbulence in fluids. We trace the post-bifurcational development of this instability beyond the limits of app! licabilit y of scale free continuum elasticity and use a phase-field approach to capture the scale dependent sub-continuum strain localization, signaling the formation of actual cracks.
You may also like
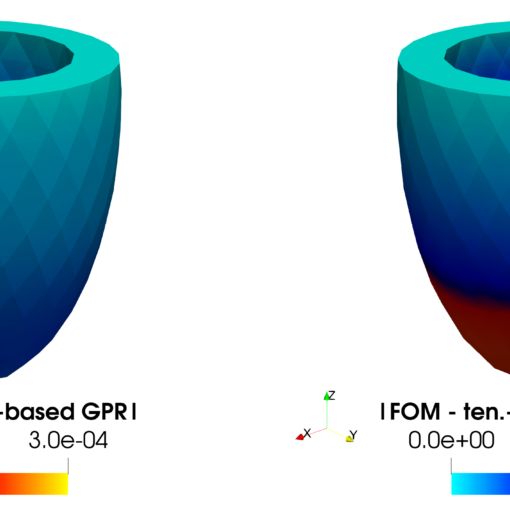
A new MOX Report entitled “Uncertainty quantification for nonlinear solid mechanics using reduced order models with Gaussian process regression” by Cicci, L.; […]
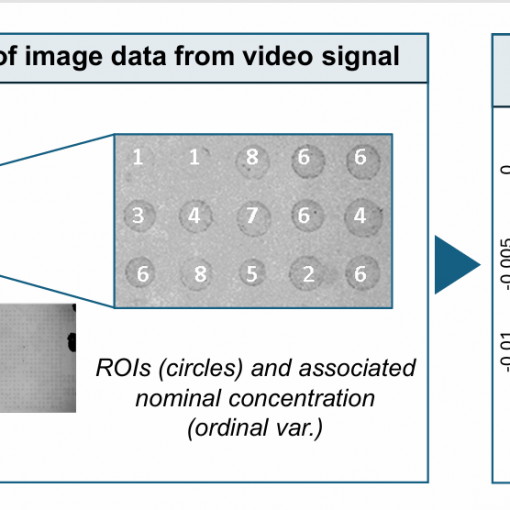
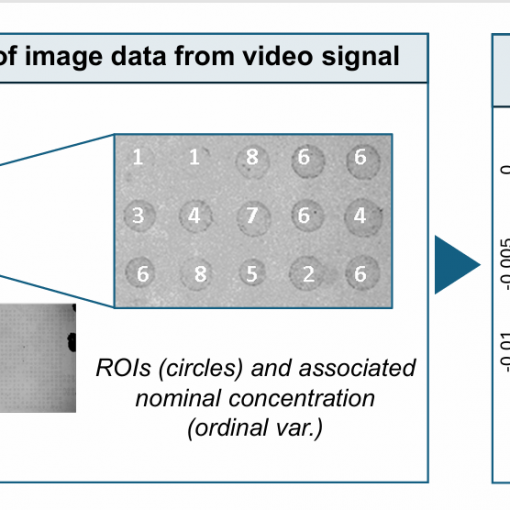
A new MOX Report entitled “Functional-Ordinal Canonical Correlation Analysis With Application to Data from Optical Sensors” by Patanè, G.; Nicolussi, F.; Krauth, […]
A new MOX Report entitled “Functional-Ordinal Canonical Correlation Analysis With Application to Data from Optical Sensors” by Patanè, G.; Nicolussi, F.; Krauth, […]
A new MOX Report entitled “Designing novel vascular stents with enhanced mechanical behavior through topology optimization of existing devices” by Ferro, N.; […]