A new MOX Report entitled “Uncertainty quantification for nonlinear solid mechanics using reduced order models with Gaussian process regression” by Cicci, L.; Fresca, S.; Guo, M.; Manzoni, A.; Zunino, P. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/105-2023.pdf
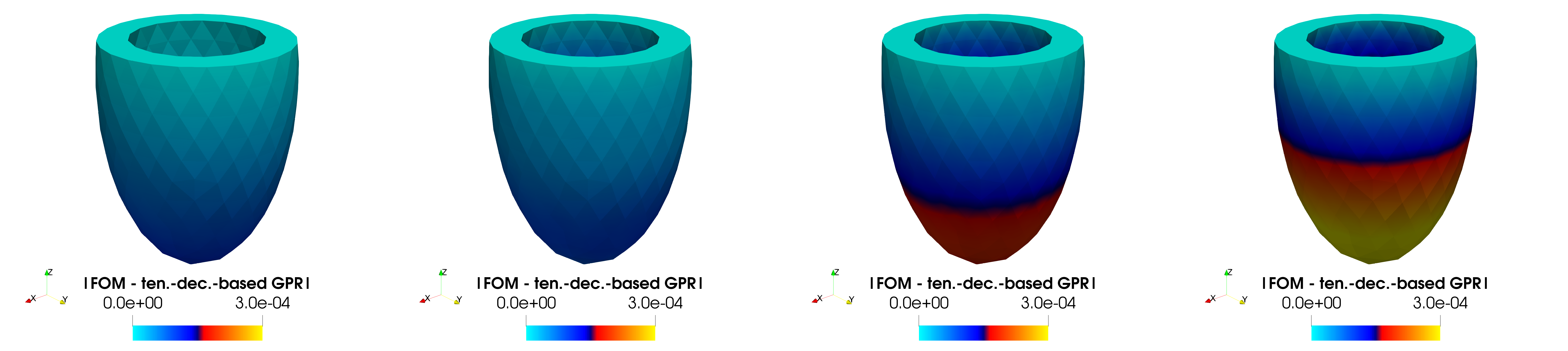
Abstract: Uncertainty quantification (UQ) tasks, such as sensitivity analysis and parameter estimation, entail a huge computational complexity when dealing with input-output maps involving the solution of nonlinear differential problems, because of the need to query expensive numerical solvers repeatedly. Projection-based reduced order models (ROMs), such as the Galerkin-reduced basis (RB) method, have been extensively developed in the last decades to overcome the computational complexity of high fidelity full order models (FOMs), providing remarkable speed-ups when addressing UQ tasks related with parameterized differential problems. Nonetheless, constructing a projection-based ROM that can be efficiently queried usually requires extensive modifications to the original code, a task which is non-trivial for nonlinear problems, or even not possible at all when proprietary software is used. Non-intrusive ROMs – which rely on the FOM as a black box – ha! ve been r ecently developed to overcome this issue. In this work, we consider ROMs exploiting proper orthogonal decomposition to construct a reduced basis from a set of FOM snapshots, and Gaussian process regression (GPR) to approximate the RB projection coefficients. Two different approaches, namely a global GPR and a tensor-decomposition-based GPR, are explored on a set of 3D time-dependent solid mechanics examples. Finally, the non-intrusive ROM is exploited to perform global sensitivity analysis (relying on both screening and variance-based methods) and parameter estimation (through Markov chain Monte Carlo methods), showing remarkable computational speed-ups and very good accuracy compared to high-fidelity FOMs.