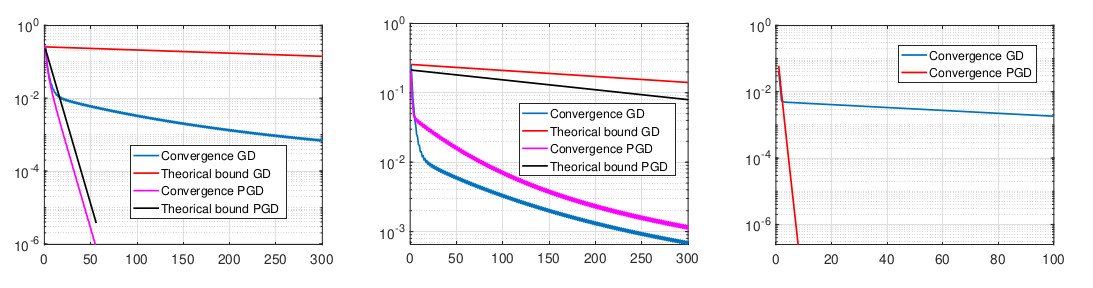
A new MOX Report entitled “Variable reduction as a nonlinear preconditioning approach for optimization problems” by Ciaramella, G.; Vanzan, T. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/58-2024.pdf Abstract: When considering an unconstrained minimization problem, a standard approach is to solve the optimality system with a Newton method possibly preconditioned by, e.g., nonlinear elimination. In this contribution, we argue that nonlinear elimination could be used to reduce the number of optimization variables by artificially constraining them to satisfy a subset of the optimality conditions. Consequently, a reduced objective function is derived which can now be minimized with any optimization algorithm. By choosing suitable variables to eliminate, the conditioning of the reduced optimization problem is largely improved. We here focus in particular on a right preconditioned gradient descent and show theoretical and numerical results supporting the validity of the presented approach.
