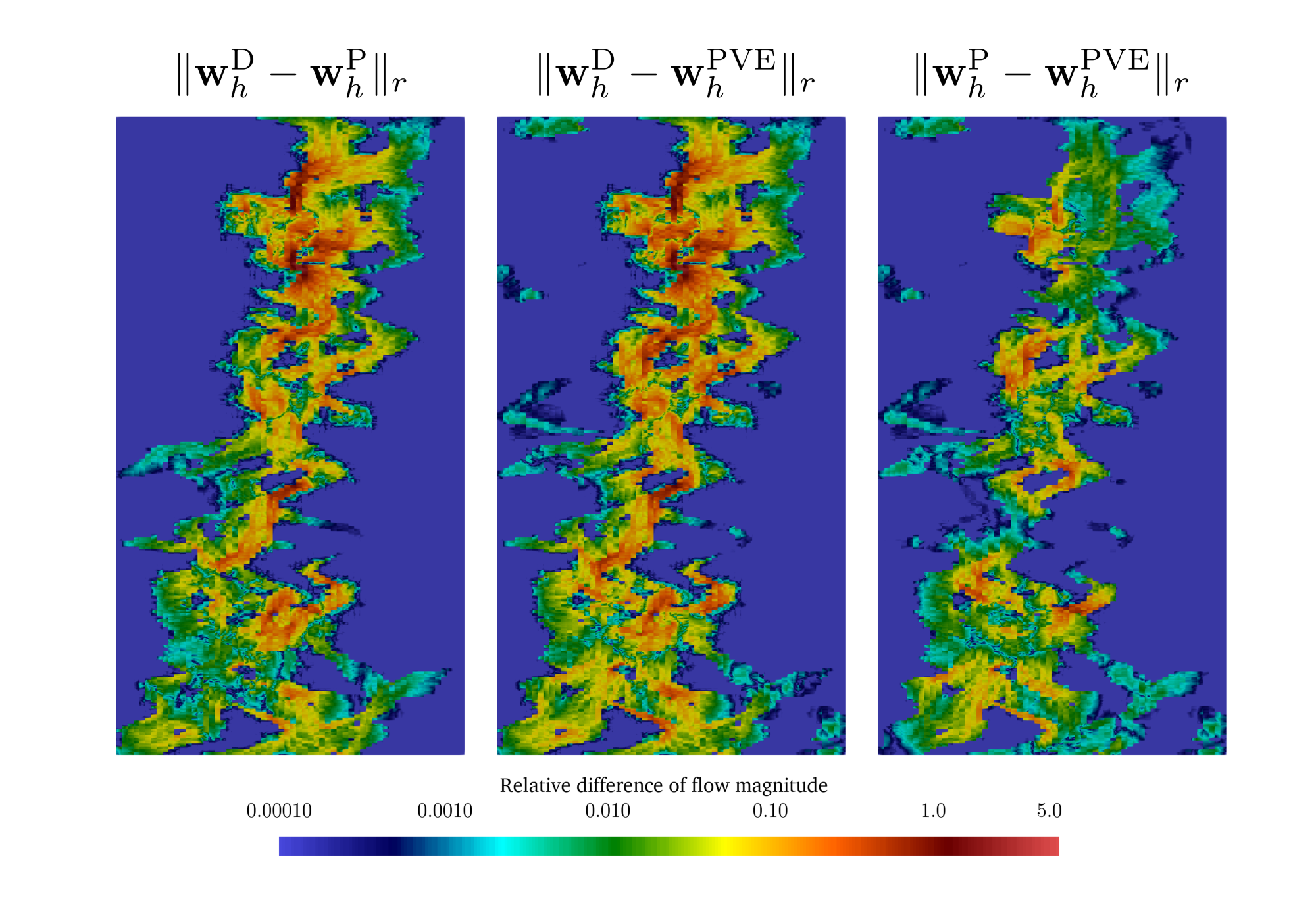
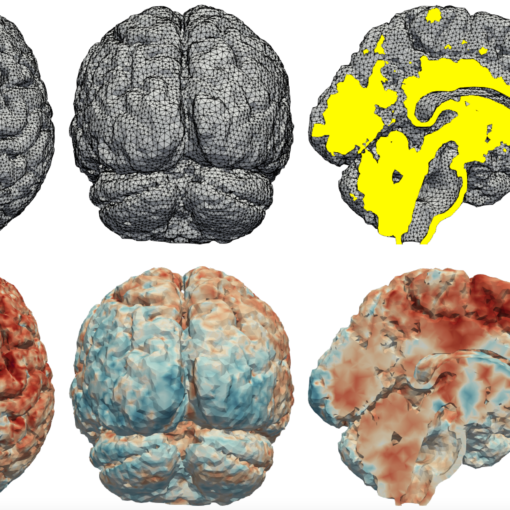
A new MOX Report entitled “Unified discontinuous Galerkin analysis of a thermo/poro-viscoelasticity model” by Bonetti, S.; Corti, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/101-2024.pdf Abstract: We present and analyze a discontinuous Galerkin method for the numerical modeling of a Kelvin-Voigt thermo/poro-viscoelastic problem. We present the derivation of the model, and we develop a stability analysis in the continuous setting that holds both for the full inertial and quasi-static problems and that is robust with respect to most of the physical parameters of the problem. For spatial discretization, we propose an arbitrary-order weighted symmetric interior penalty scheme that supports general polytopal grids and is robust with respect to strong heterogeneities in the model coefficients. For the semi-discrete problem, we prove the extension of the stability result demonstrated in the continuous setting. A wide set of numerical simulations is presented to assess the convergence and robustness properties of the proposed method. Moreover, we test the scheme with literature and physically sound test cases for proof-of-concept applications in t! he geophy sical context.
You may also like
A new MOX Report entitled “Analyzing data in complicated 3D domains: smoothing, semiparametric regression and functional principal component analysis” by Arnone, E.; […]
A new MOX Report entitled “Designing novel vascular stents with enhanced mechanical behavior through topology optimization of existing devices” by Ferro, N.; […]
A new MOX Report entitled “A PCA and mesh adaptation-based format for high compression of Earth Observation optical data with applications in […]
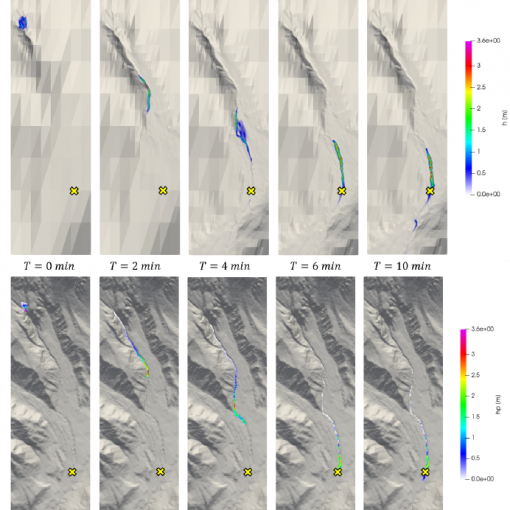
A new MOX Report entitled “A comparative analysis of mesh-based and particle-based numerical methods for landslide run-out simulations” by Fois, M.; Gatti, […]