A new MOX Report entitled “Telescopic quantum simulation of the advection-diffusion-reaction dynamics” by Zecchi, A. A.; Sanavio, C.; Perotto, S.; Succi, S. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/53-2025.pdf
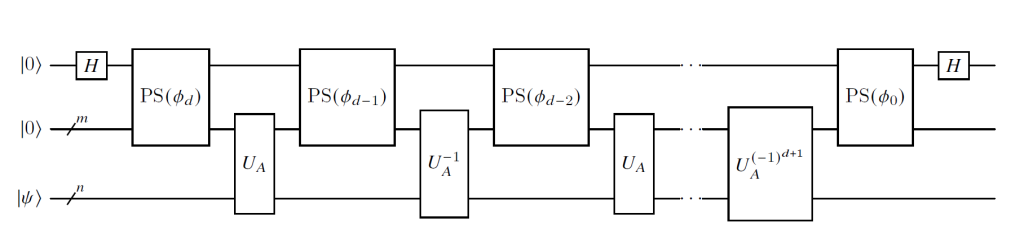
Abstract: Quantum singular value transformation (QSVT) is a powerful technique that applies a polynomial transformation to the singular values of a matrix encoded in a unitary operator. Many quantum algorithms can be viewed as a particular application of this technique, though its application to the quantum computation of classical dynamics has not been extensively explored. We introduce a telescopic quantum algorithm for solving the advection-diffusion-reaction (ADR) equation at a given (possibly large) final simulation time, applying the QSVT to an efficient block-encoding of the matrix representing the considered dynamics. We decompose the ADR time evolution function using a Chebyshev polynomial of degree d and we show that effectively exploiting the spectral knowledge of the input matrix within the QSVT protocol can provide a similar simulation error with up to an order of magnitude lower of polynomial degree. The associated quantum circuit employs only n+4 qubits where N=2^n is the number of spatial discretization points, and achieves circuit depth of O(d × poly(n)). The efficient use of quantum resources and the reduced overall complexity pave the way for the application of the proposed algorithm on near term quantum hardware.