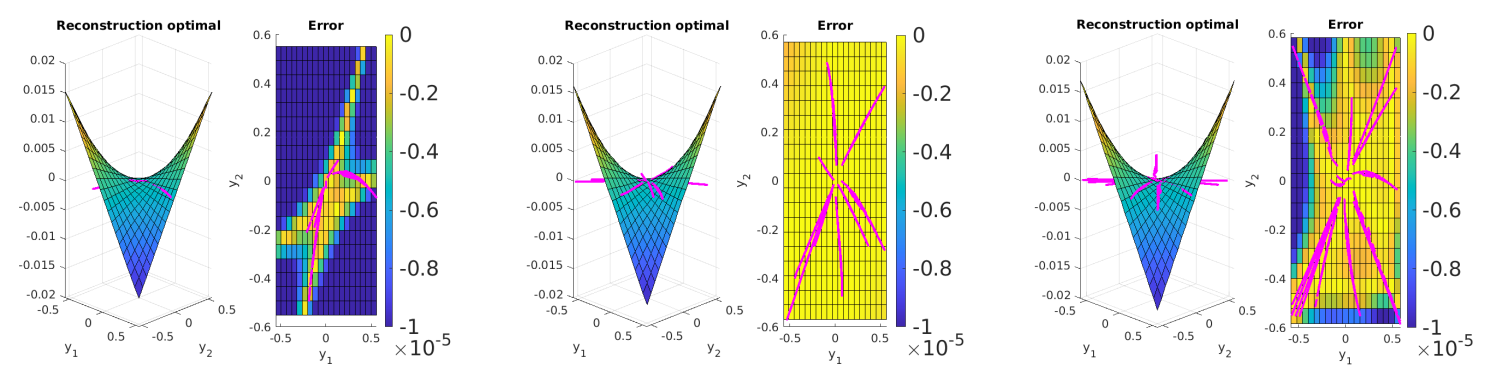
A new MOX Report entitled “Reconstruction of unknown nonlienar operators in semilinear elliptic models using optimal inputs” by Bartsch, J.; Buchwald, S.; Ciaramella, G.; Volkwein, S. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/39-2024.pdf Abstract: Physical models often contain unknown functions and relations. The goal of our work is to answer the question of how one should excite or control a system under consideration in an appropriate way to be able to reconstruct an unknown nonlinear relation. To answer this question, we propose a greedy reconstruction algorithm within an offline-online strategy. We apply this strategy to a two-dimensional semilinear elliptic model. Our identification is based on the application of several space-dependent excitations (also called controls). These specific controls are designed by the algorithm in order to obtain a deeper insight into the underlying physical problem and a more precise reconstruction of the unknown relation. We perform numerical simulations that demonstrate the effectiveness of our approach which is not limited to the current type of equation. Since our algorithm provides not only a way to determine unknown operators by existing data but ! also prot ocols for new experiments, it is a holistic concept to tackle the problem of improving physical models.
