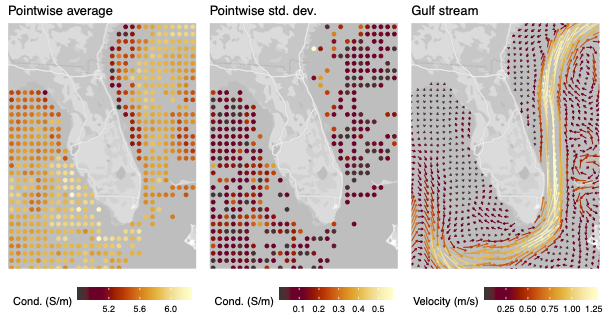
A new MOX Report entitled “PDE-regularised spatial quantile regression” by Castiglione, C.; Arnone, E.; Bernardi, M.; Farcomeni, A.; Sangalli, L.M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/98-2024.pdf Abstract: We consider the problem of estimating the conditional quantiles of an unknown distribution from data gathered on a spatial domain. We propose a spatial quantile regression model with differential regularisation. The penalisation involves a partial differential equation defined over the considered spatial domain, that can display a complex geometry. Such regularisation permits, on one hand, to model complex anisotropy and non-stationarity patterns, possibly on the basis of problem-specific knowledge, and, on the other hand, to comply with the complex conformation of the spatial domain. We define an innovative functional Expectation-Maximisation algorithm, to estimate the unknown quantile surface. We moreover describe a suitable discretisation of the estimation problem, and investigate the theoretical properties of the resulting estimator. The performance of the proposed method is assessed by simulation studies, comparing with state-of-the-art tech! niques fo r spatial quantile regression. Finally, the considered model is applied to two real data analyses, the first concerning rainfall measurements in Switzerland and the second concerning sea surface conductivity data in the Gulf of Mexico.
You may also like
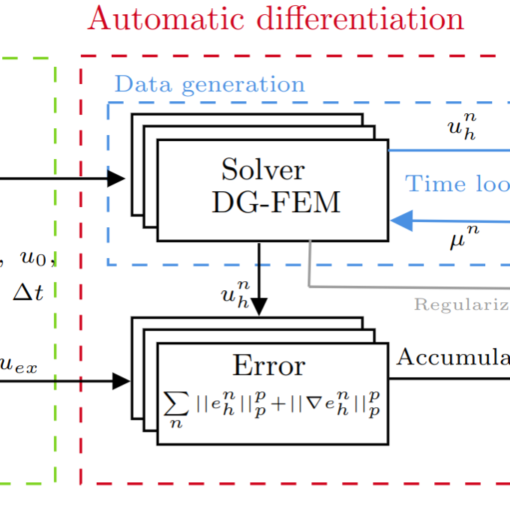
A new MOX Report entitled “Discovering Artificial Viscosity Models for Discontinuous Galerkin Approximation of Conservation Laws using Physics-Informed Machine Learning” by Caldana, […]
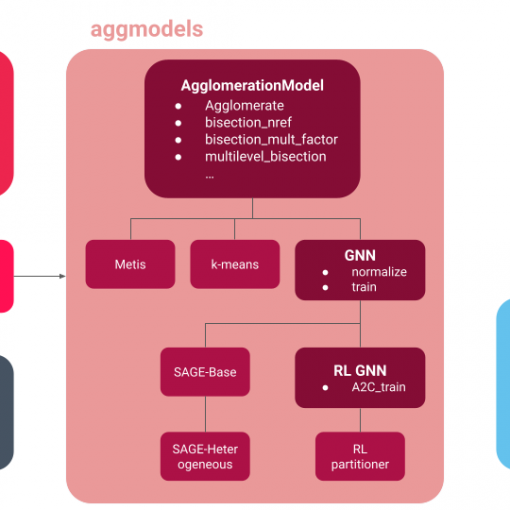
A new MOX Report entitled “MAGNET: an open-source library for mesh agglomeration by Graph Neural Networks” by Antonietti, P. F.; Caldana, M.; […]
A new MOX Report entitled “A staggered-in-time and non-conforming-in-space numerical framework for realistic cardiac electrophysiology outputs” by Zappon, E.; Manzoni, A.; Quarteroni, […]
A new MOX Report entitled “A comprehensive stroke risk assessment by combining atrial computational fluid dynamics simulations and functional patient data” by […]