A new MOX Report entitled “Optimal surface clothing with elastic nets” by Andrini, D.; Magri, M.; Ciarletta, P. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/93-2023.pdf
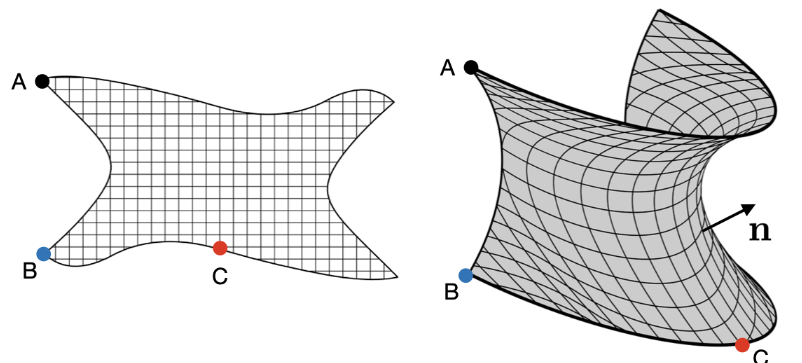
Abstract: The clothing problem aims at identifying the shape of a planar fabric for covering a target surface in the three-dimensional space. It poses significant challenges in various applications, ranging from fashion industry to digital manufacturing. Here, we propose a novel inverse design approach to the elastic clothing problem that is formulated as a constrained optimization problem. We assume that the textile behaves as an orthotropic, nonlinear elastic surface with fibers distributed along its warp and weft threads, and we enforce mechanical equilibrium as a variational problem. The target surface is frictionless, except at its boundary where the textile is pinned, imposing a unilateral obstacle condition for the reactive forces at the target surface. The constrained optimization problem also accounts for an elongation condition of the warp and weft fibers, possibly with bounded shearing angle. We numerically solve the resulting constraine! d optimiz ation problem by means of a gradient descent algorithm. The numerical results are first validated against known clothing solutions for Chebyshev nets, taking the limit of inextensible fibers. We later unravel the interplay between thread and shear stiffness for driving the optimal cloth shape covering the hemisphere and the hemicatenoid. We show how the metric of these target surfaces strongly affects the resulting distribution of the reaction forces. When considering the limit of covering the full sphere, we show how clothing with elastic nets allows to avoid the onset of singularities in the corresponding Chebyshev net, by developing corners at the cloth boundary.