A new MOX Report entitled “On the inf-sup condition for Hierarchical Model reduction of the Stokes problem” by Temellini, E.; Ballarin, F.; Chacon Rebollo, T.; Perotto, S. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/48-2025.pdf
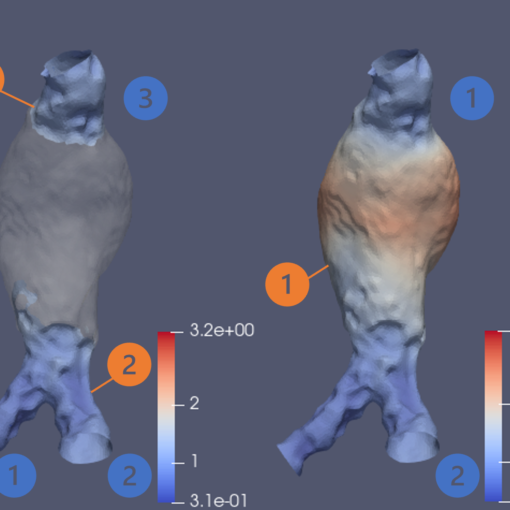
Abstract: Hierarchical Model Reduction is an effective Reduced Order Modelling technique for problems defined on elongated, pipe-like domains. It is particularly suitable when a dominant dynamics is aligned with the longitudinal direction, while transverse effects are locally significant but spatially limited. When applied to two-field problems such as the Stokes equations, a main challenge is to ensure the stability of the reduced formulation, particularly the inf-sup condition for pressure discretization. In this work, we provide a rigorous analysis showing that the inf-sup condition holds whenever the number of velocity modes is at least equal to the number of pressure modes, thereby extending previous heuristic approaches. The proof exploits the separation of variables in HiMod and is valid for pipe-like domains under some geometric assumptions. Numerical assessment confirms the theoretical findings, providing a solid foundation for stable and efficient HiMod reduction in incompressible flow problems.