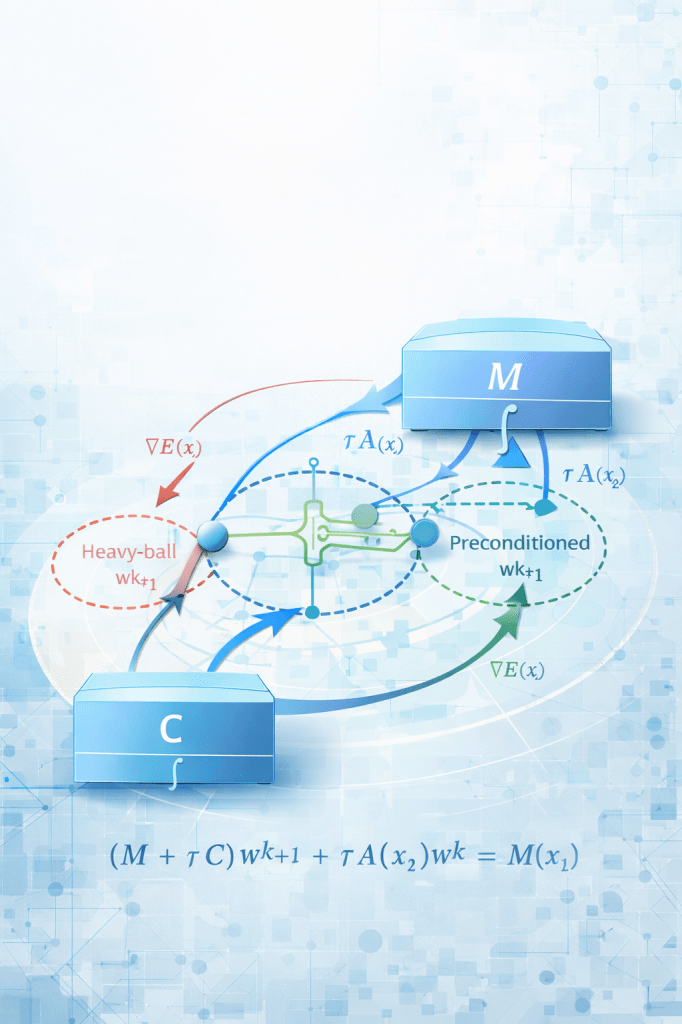
A new MOX Report entitled ” Newmark time marching as a preconditioned iteration for large SPD linear systems ” by Micheletti, S. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/08-2026.pdf
Abstract: We revisit the classical idea of computing the solution of a large symmetric positive definite linear system as the steady state of an artificial transient dynamics. Starting from a second-order model with “mass” and “damping” operators, we show that the explicit Newmark scheme (beta=0) induces a family of stationary iterations for Au=b, with a natural residual form and a transparent role for the pair (M, C). This viewpoint unifies, within a single algebraic framework, time-marching solvers, preconditioned fixed-point iterations, and momentum-like recurrences. In particular, by choosing M as a preconditioner and using Rayleigh damping C = a_0 M + a_1 A, the induced iteration can be implemented efficiently via inexact inner solves and behaves as a robust preconditioned method for challenging diffusion problems. Numerical experiments on model elliptic operators illustrate the influence of (M, C) and provide practical parameter guidelin! es.