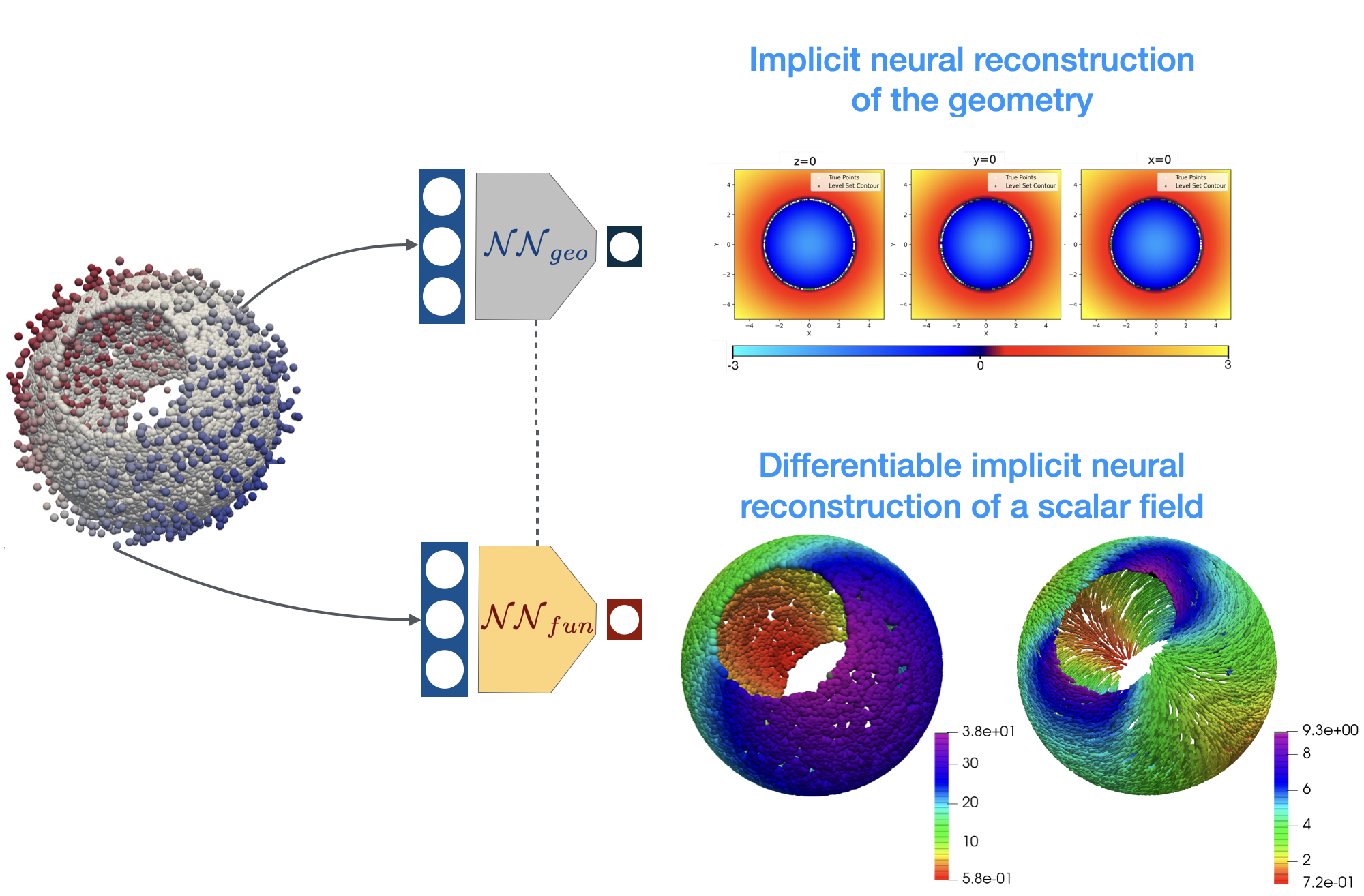
A new MOX Report entitled “Implicit neural field reconstruction on complex shapes from scattered and noisy data” by Carrara, D.; Regazzoni, F.; Pagani, S. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/40-2024.pdf Abstract: Reconstructing distributed physical quantities from scattered sensor data is a challenging task due to geometric and measurement uncertainties. We propose a novel machine learning based framework that allows to implicitly represent geometries solely from noisy surface points, by training a neural network model in a semi-supervised manner. We investigate different combinations of regularizing terms for the loss function, including a differential one based on the Eikonal equation, thus ensuring that the level set function approximates a signed distance function without the need for preprocessing data. This makes the method suitable for realistic, noise-corrupted, and sparse data. Furthermore, our approach leverages neural networks to predict distributed quantities defined on surfaces, while ensuring geometrical compatibility with the underlying implicit geometry representation. Our approach allows for accurate reconstruction of derived quantities s! uch as su rface gradients by relying on automatic differentiation tools. Comprehensive tests on synthetic data validate the method’s efficacy, which demonstrate its potential for significant applications in healthcare.
You may also like
A new MOX Report entitled “Multi-state Modeling of Delay Evolution in Suburban Rail Transports” by Colombo, S.; Gimenez Zapiola, A.; Ieva, F.; […]
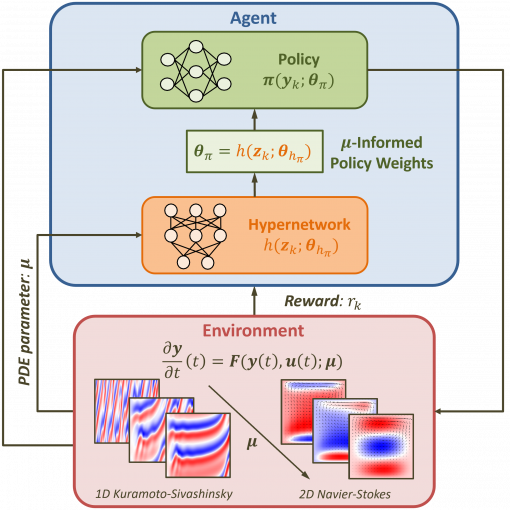
A new MOX Report entitled “HypeRL: Parameter-Informed Reinforcement Learning for Parametric PDEs” by Botteghi, N.; Fresca, S.; Guo, M.; Manzoni, A. has […]
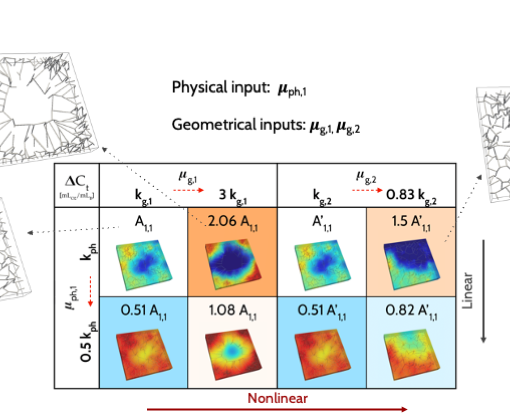
A new MOX Report entitled “Sensitivity analysis of a multi-physics model for the vascular microenvironment” by Vitullo, P.; Cicci, L.; Possenti, L.; […]
A new MOX Report entitled “Efficient particle generation for depth-averaged and fully 3D MPM using TIFF image data” by Fois, M.; de […]