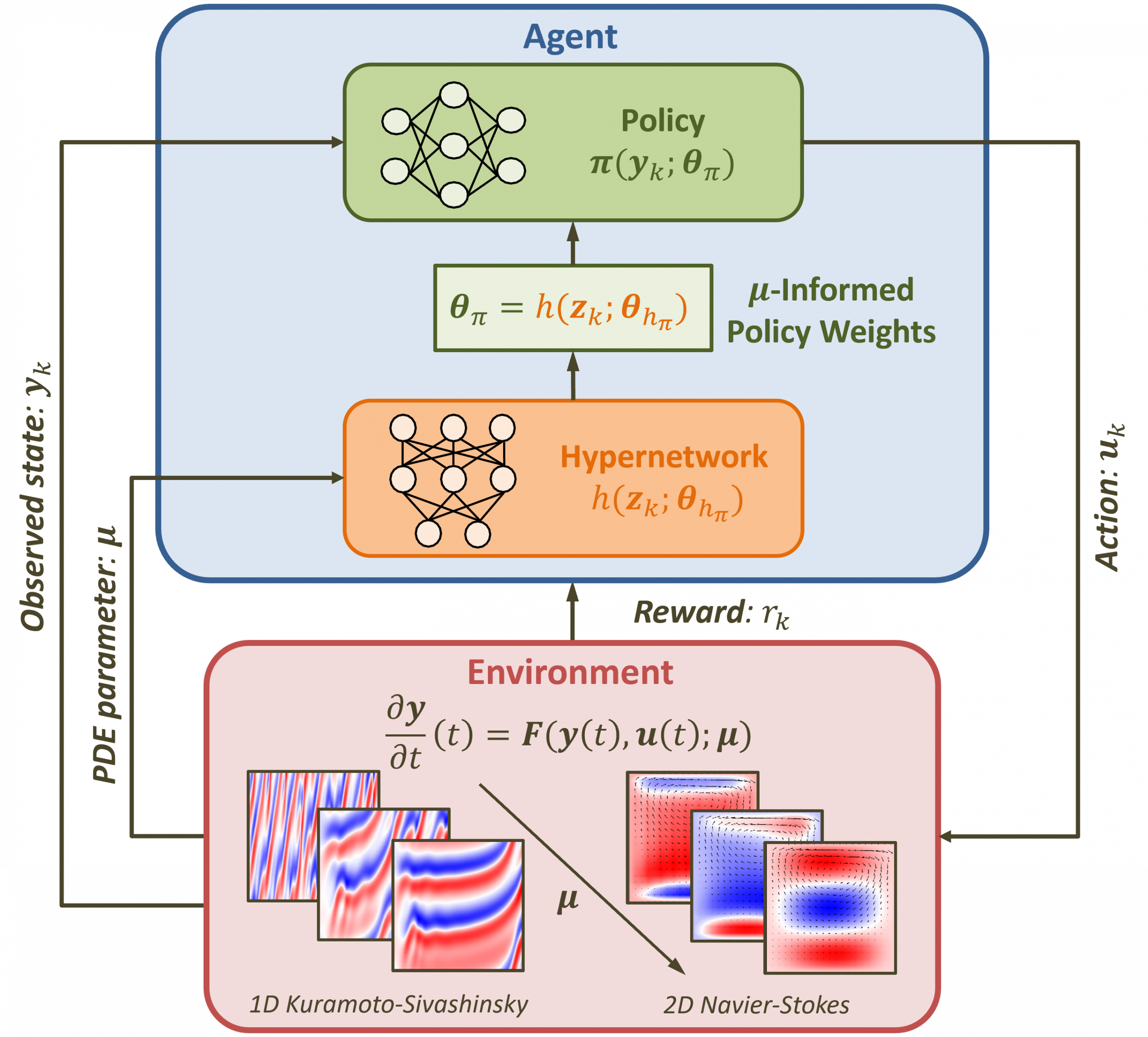
A new MOX Report entitled “HypeRL: Parameter-Informed Reinforcement Learning for Parametric PDEs” by Botteghi, N.; Fresca, S.; Guo, M.; Manzoni, A. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/31-2025.pdf
Abstract: In this work, we devise a new, general-purpose reinforcement learning strategy for the optimal control of parametric partial differential equations (PDEs). Such problems frequently arise in applied sciences and engineering and entail a significant complexity when control and or state variables are distributed in high- dimensional space or depend on varying parameters. Traditional numerical methods, relying on either iterative minimization algorithms – exploiting, e.g., the solution of the adjoint problem – or dynamic programming – also involving the solution of the Hamilton-Jacobi-Bellman (HJB) equation – while reliable, often become computationally infeasible. Indeed, in either way, the optimal control problem has to be solved for each instance of the parameters, and this is out of reach when dealing with high-dimensional time-dependent and parametric PDEs. In this paper, we propose HypeRL, a deep reinforcement learning (DRL) framework ! to overco me the limitations shown by traditional methods. HypeRL aims at approximating the optimal control policy directly, bypassing the need to numerically solve the HJB equation explicitly for all possible states and parameters, or solving an adjoint problem within an iterative optimization loop for each parameter instance. Specifically, we employ an actor-critic DRL approach to learn an optimal feedback control strategy that can generalize across the range of variation of the parameters. To effectively learn such optimal control laws for different instances of the parameters, encoding the parameter information into the DRL policy and value function neural networks (NNs) is essential. To do so, HypeRL uses two additional NNs, often called hypernetworks, to learn the weights and biases of the value function and the policy NNs. In this way, HypeRL effectively embeds the parametric information into the value function and policy NNs. We validate the proposed approach on two PDE-const! rained op timal control benchmarks, namely a 1D Kuramoto-Sivashinsky equation with in-domain control and on a 2D Navier Stokes equations with boundary control, by showing that the knowledge of the PDE parameters and how this information is encoded, i.e., via a hypernetwork, is an essential ingredient for learning parameter-dependent control policies that can generalize effectively to unseen scenarios and for improving the sample efficiency of such policies.