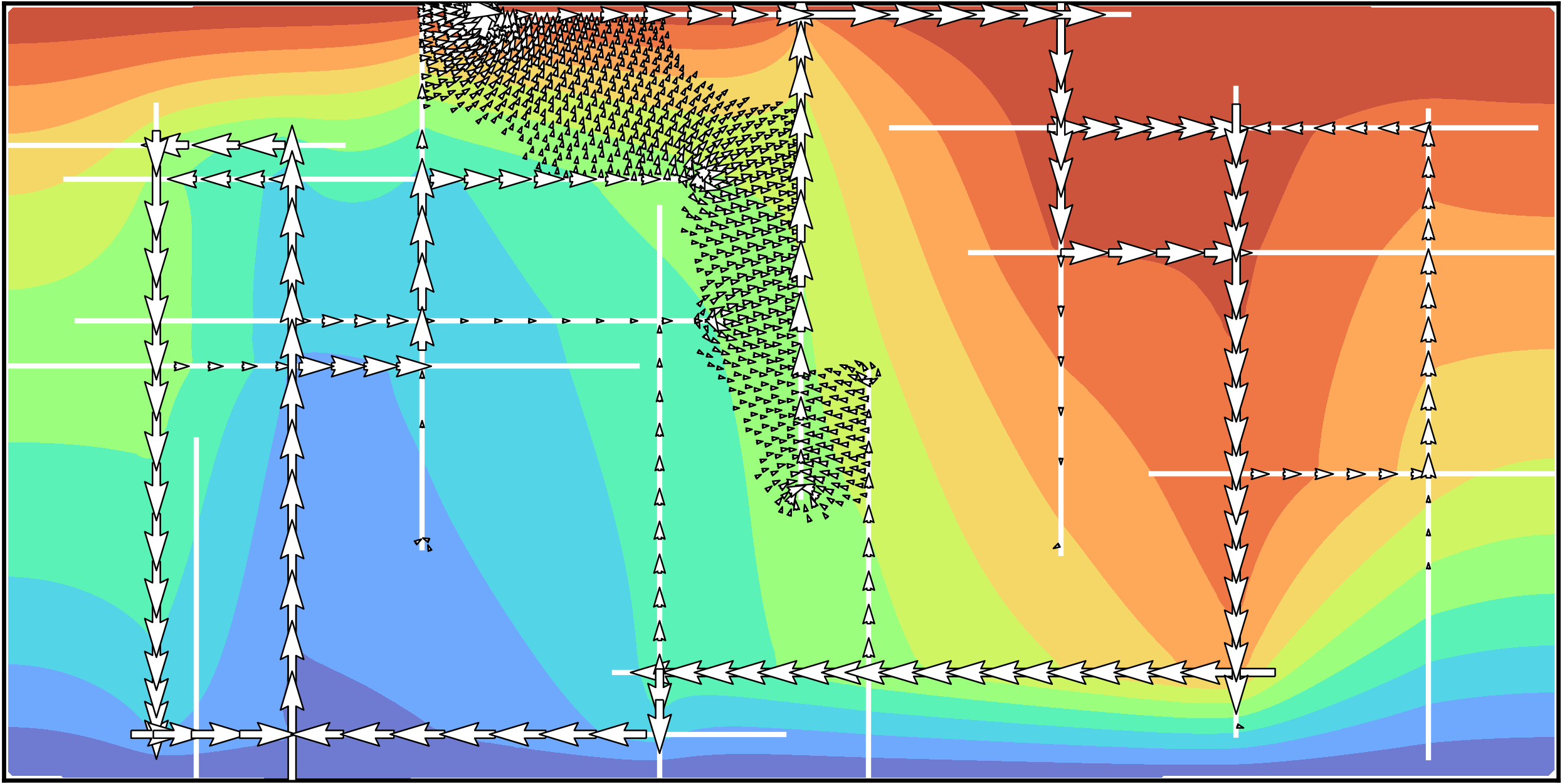
A new MOX Report entitled “Free convection in fractured porous media: a numerical study ” by Roknian, A.A.; Scotti, A.; Fumagalli, A. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/62-2024.pdf Abstract: The objective of this study is to better understand the influence of fractures on the possibility of free convection in porous media. To this aim, we introduce a mathematical model for density driven flow in the presence of fractures, and the corresponding numerical approximation. In addition to the direct numerical solution of the problem we propose and implement a novel method for the assessment of convective stability through the eigenvalue analysis of the linearized numerical problem. The new method is shown to be in agreement with existing literature cases both in simple and complex fracture configurations. With respect to direct simulation in time, the results of the eigenvalue method lack information about the strength of convection and the steady state solution, they however provide detailed (quantitative) information about the behavior of the solution near the initial equilibrium condition. Furthermore, not having to solve a time-depende! nt proble m makes the method computationally very efficient. Finally, the question of how the porous matrix interacts with the fracture network to enable free convection is examined: the porous matrix is shown to be of key importance in enabling convection for complex fracture networks, making stability criteria based on the fracture network alone somewhat limited in applicability.
