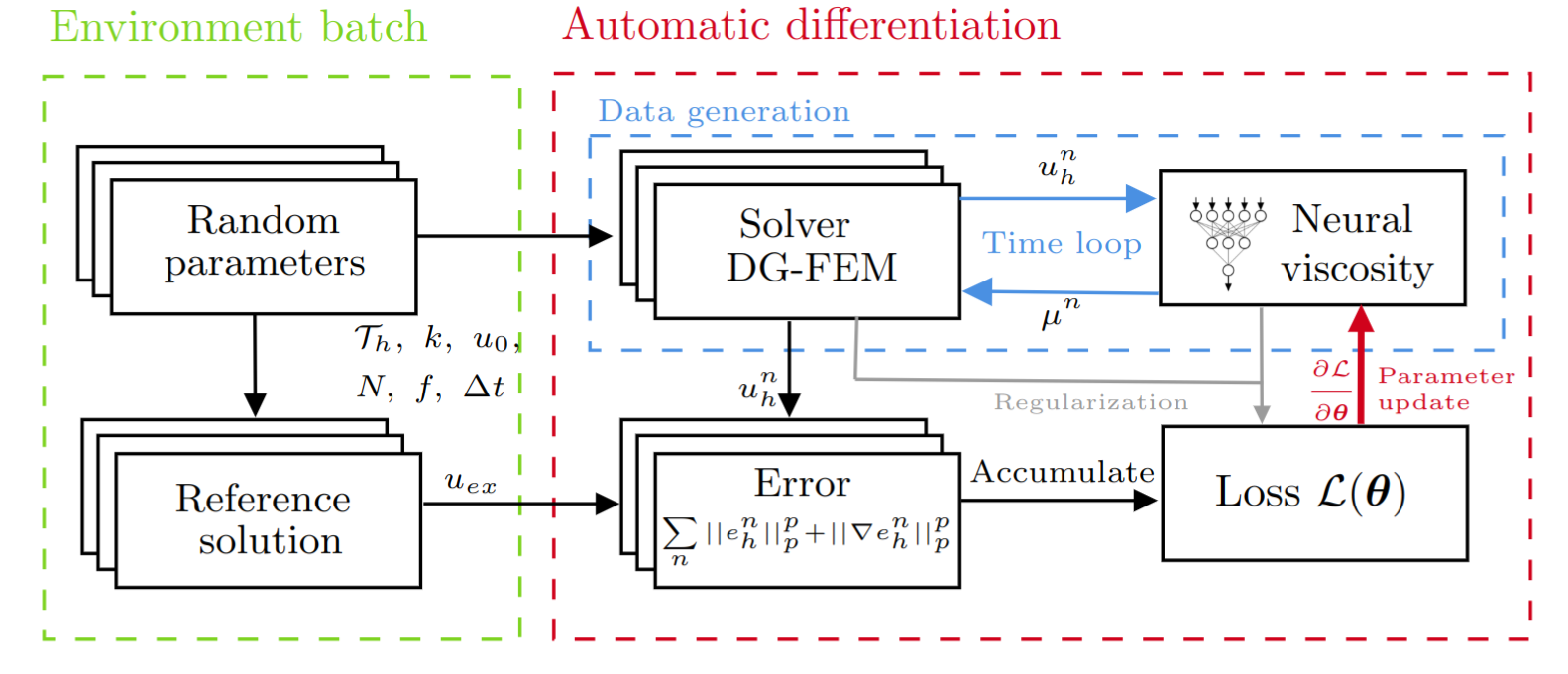
A new MOX Report entitled “Discovering Artificial Viscosity Models for Discontinuous Galerkin Approximation of Conservation Laws using Physics-Informed Machine Learning” by Caldana, M.; Antonietti P. F.; Dede’ L. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/21-2024.pdf
Abstract: Finite element-based high-order solvers of conservation laws offer large accuracy but face challenges near discontinuities due to the Gibbs phenomenon. Artificial viscosity is a popular and effective solution to this problem based on physical insight. In this work, we present a physics-informed machine learning algorithm to automate the discovery of artificial viscosity models in a non-supervised paradigm. The algorithm is inspired by reinforcement learning and trains a neural network acting cell-by-cell (the viscosity model) by minimizing a loss defined as the difference with respect to a reference solution thanks to automatic differentiation. This enables a dataset-free training procedure. We prove that the algorithm is effective by integrating it into a state-of-the-art Runge-Kutta discontinuous Galerkin solver. We showcase several numerical tests on scalar and vectorial problems, such as Burgers’ and Euler’s equations in one and two dimensi! ons. Resu lts demonstrate that the proposed approach trains a model that is able to outperform classical viscosity models. Moreover, we show that the learnt artificial viscosity model is able to generalize across different problems and parameters.