A new MOX Report entitled “Discontinuous Galerkin time integration for second-order differential problems: formulations, analysis, and analogies” by Ciaramella, G.; Gander, M.J.; Mazzieri, I. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/28-2025.pdf
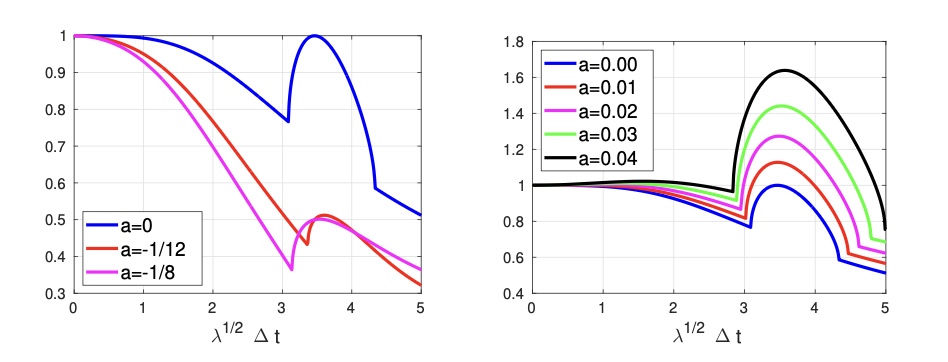
Abstract: We thoroughly investigate Discontinuous Galerkin (DG) discretizations as time integrators for second-order oscillatory systems, considering both second-order and first-order formulations of the original problem. Key contributions include new convergence analyses for the second-order formulation and equivalence proofs between DG and classical time-stepping schemes (such as Newmark schemes and general linear methods). In addition, the chapter provides a detailed review and convergence analysis for the first-order formulation, alongside comparisons of the proposed schemes in terms of accuracy, consistency, and computational cost