A new MOX Report entitled “Discontinuous Galerkin for the heterodimer model of prion dynamics in Parkinson’s disease” by Antonietti, P.F.; Bonizzoni, F.; Corti, M.; Dall’Olio, A. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/78-2023.pdf
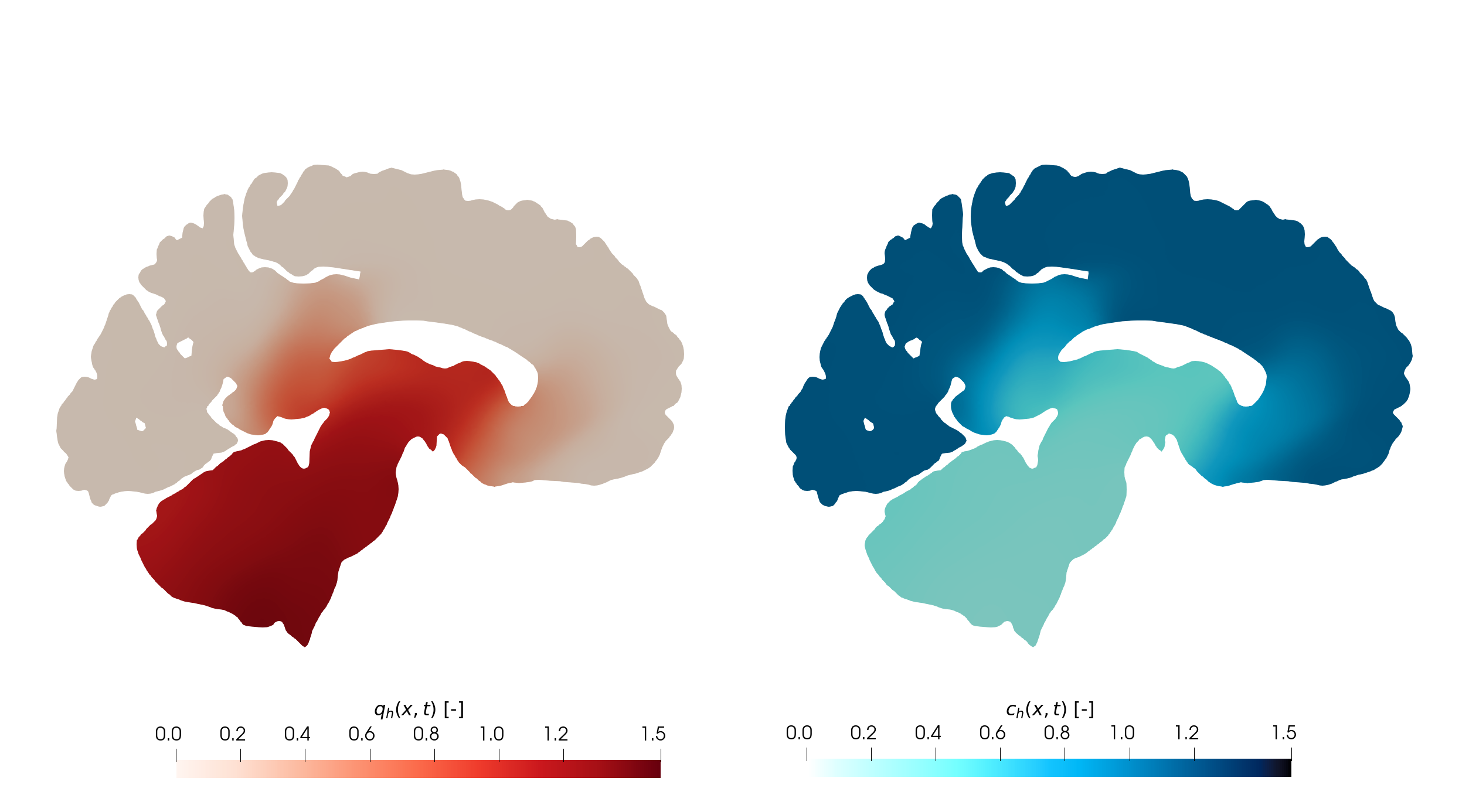
Abstract: Neurodegenerative diseases have a significant global impact affecting millions of individuals worldwide. Some of them, known as proteinopathies, are characterized by the accumulation and propagation of toxic proteins, known as prions. Alzheimer’s and Parkinson’s diseases are relevant of protheinopathies. Mathematical models of prion dynamics play a crucial role in understanding disease progression and could be of help to potential interventions. This article focuses on the heterodimer model: a system of two partial differential equations that describe the evolution of healthy and misfolded proteins. In particular, we propose a space discretization based on a Discontinuous Galerkin method on polygonal/polyhedral grids, which provides flexibility in handling meshes of complex brain geometries. Concerning the semi-discrete formulation we prove stability and a-priori error estimates. Next, we adopt a theta-method scheme for time discretization. Som! e converg ence tests are performed to confirm the theoretical bounds and the ability of the method to approximate travelling wave solutions. The proposed scheme is also tested to simulate the spread of alpha-synuclein in a realistic test case of Parkinson’s disease in a two-dimensional sagittal brain section geometry reconstructed from medical images.