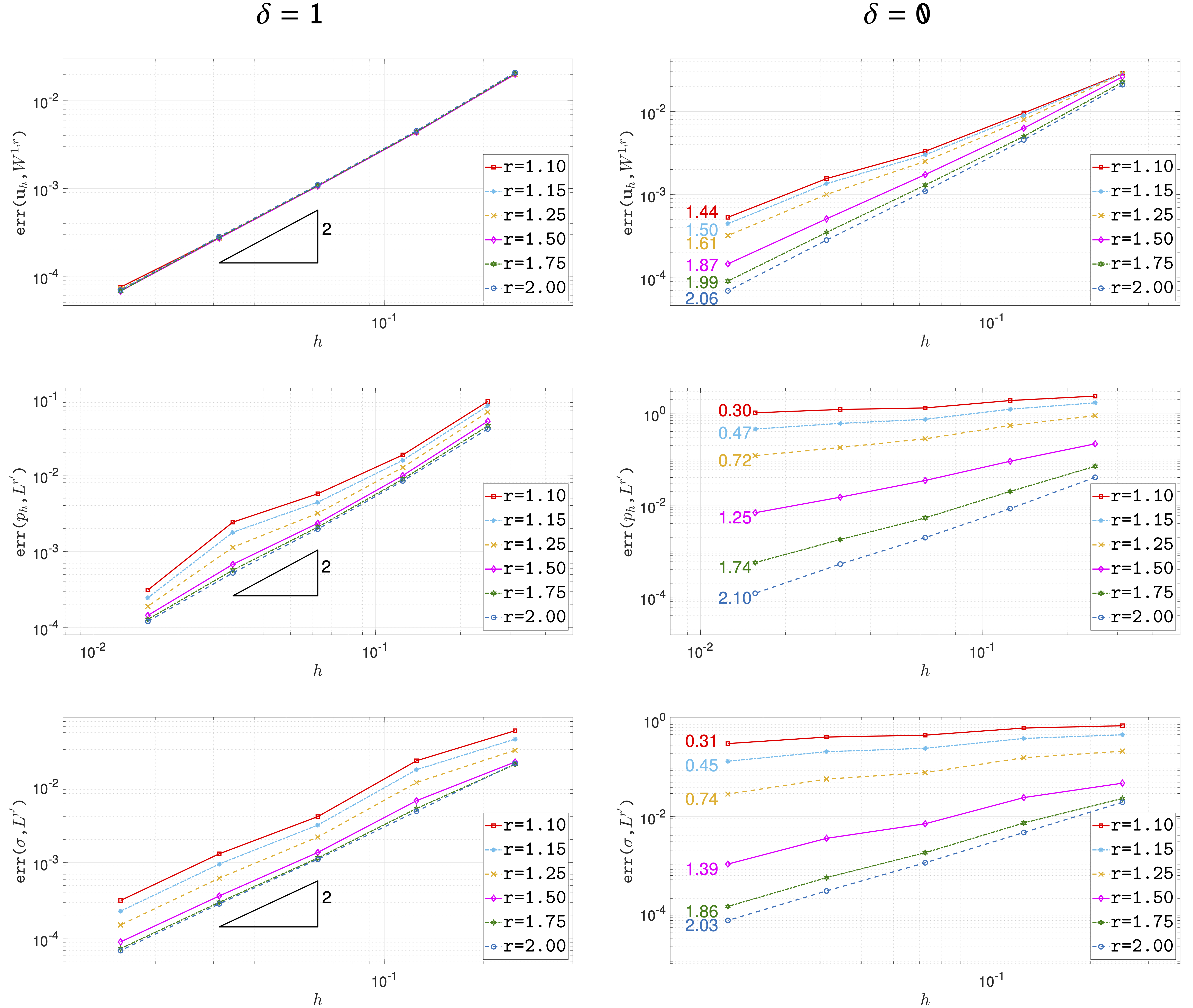
A new MOX Report entitled “A Virtual Element method for non-Newtonian fluid flows” by Antonietti, P.F.; Beirao da Veiga, L.; Botti, M.; Vacca, G.; Verani, M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/27-2024.pdf Abstract: In this paper, we design and analyze a Virtual Element discretization for the steady motion of non-Newtonian, incompressible fluids. A specific stabilization, tailored to mimic the monotonicity and boundedness properties of the continuous operator, is introduced and theoretically investigated. The proposed method has several appealing features, including the exact enforcement of the divergence free condition and the possibility of making use of fully general polygonal meshes. A complete well-posedness and convergence analysis of the proposed method is presented under mild assumptions on the non-linear laws, encompassing common examples such as the Carreau–Yasuda model. Numerical experiments validating the theoretical bounds as well as demonstrating the practical capabilities of the proposed formulation are presented.
You may also like
A new MOX Report entitled “A staggered-in-time and non-conforming-in-space numerical framework for realistic cardiac electrophysiology outputs” by Zappon, E.; Manzoni, A.; Quarteroni, […]
A new MOX Report entitled “Telescopic quantum simulation of the advection-diffusion-reaction dynamics” by Zecchi, A. A.; Sanavio, C.; Perotto, S.; Succi, S. […]
A new MOX Report entitled “Assessing the Impact of Hybrid Teaching on Students’ Academic Performance via Multilevel Propensity Score-based techniques” by Ragni, […]
A new MOX Report entitled “On latent dynamics learning in nonlinear reduced order modeling” by Farenga, N.; Fresca, S.; Brivio, S.; Manzoni, […]