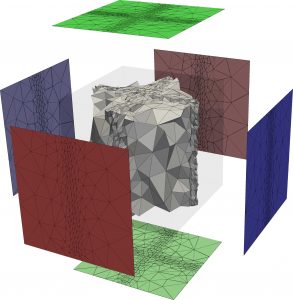
A new MOX Report entitled “A novel metric – based mesh adaptation algorithm for 3D periodic domains” by Speroni, G.; Ferro, N. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/61-2024.pdf Abstract: We present a novel metric-based mesh adaptation algorithm, named 3DPAMA, to be employed for discretization of three-dimensional periodic domains. The proposed method – based on mathematically rigorous assumptions – utilizes established techniques for unconstrained mesh adaptation and resorts to localized manipulations on the external boundary of the mesh. In particular, the scheme comprises four steps: (i) a non-periodic initial mesh adaptation, (ii) the splitting of the obtained volumetric grid into interior and exterior tessellations, (iii) minimal local operations to yield a periodic external surface, and (iv) the assembly of the final adapted grids. To demonstrate the robustness, efficacy, and flexibility of the proposed methodology, 3DPAMA algorithm is employed in a continuous finite element setting to tackle test cases established in the literature as well as challenging scenarios that involve various periodic requirements, domain geometrie! s, and me tric fields. Finally, 3DPAMA is employed in a practical use case where mesh adaptation is tightly coupled with the solution of a time-dependent partial differential equation.