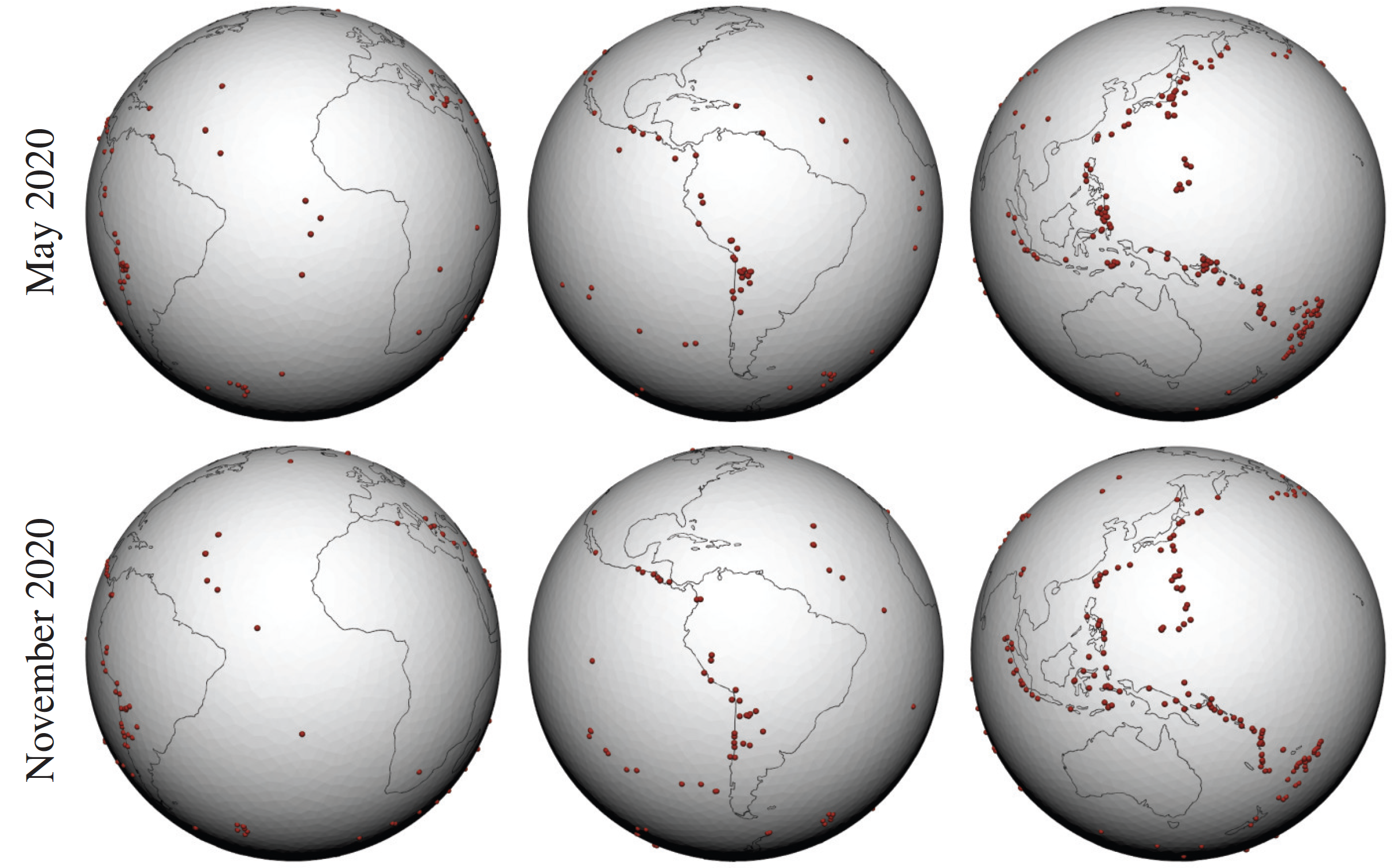
A new MOX Report entitled “A nonparametric penalized likelihood approach to density estimation of space-time point patterns” by Begu, B.; Panzeri, S.; Arnone, E.; Carey, M.; Sangalli, L.M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/37-2024.pdf Abstract: In this work, we consider space-time point processes and study their continuous space-time evolution. We propose an innovative nonparametric methodology to estimate the unknown space-time density of the point pattern, or, equivalently, to estimate the intensity of an inhomogeneous space-time Poisson point process. The presented approach combines maximum likelihood estimation with roughness penalties, based on differential operators, defined over the spatial and temporal domains of interest. We first establish some important theoretical properties of the considered estimator, including its consistency. We then develop an efficient and flexible estimation procedure that leverages advanced numerical and computation techniques. Thanks to a discretization based on finite elements in space and B–splines in time, the proposed method can effectively capture complex multi-modal and strongly anisotropic spatio-temporal point patterns; moreover, these point patterns may be observed o! ver plana r or curved domains with non-trivial geometries, due to geographic constraints, such as coastal regions with complicated shorelines, or curved regions with complex orography. In addition to providing estimates, the method’s functionalities also include the introduction of appropriate uncertainty quantification tools. We thoroughly validate the proposed method, by means of simulation studies and applications to real-world data. The obtained results highlight significant advantages over state-of-the-art competing approaches.
You may also like
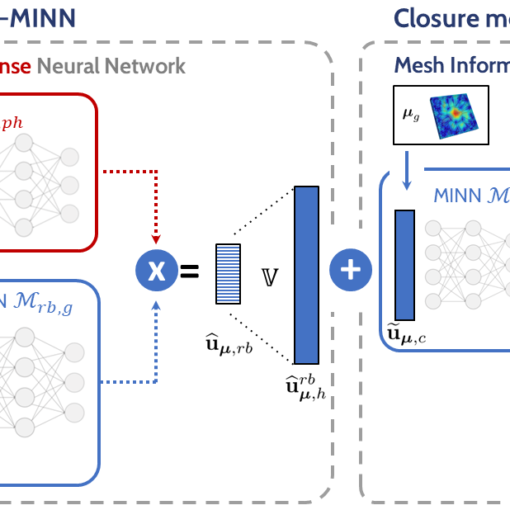
A new MOX Report entitled “Nonlinear model order reduction for problems with microstructure using mesh informed neural networks” by Vitullo, P.; Colombo, […]
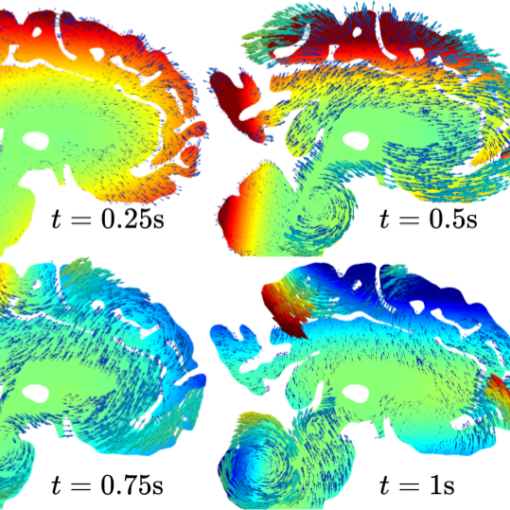
A new MOX Report entitled “Polytopal discontinuous Galerkin discretization of brain multiphysics flow dynamics” by Fumagalli, I.; Corti, M.; Parolini, N.; Antonietti, […]
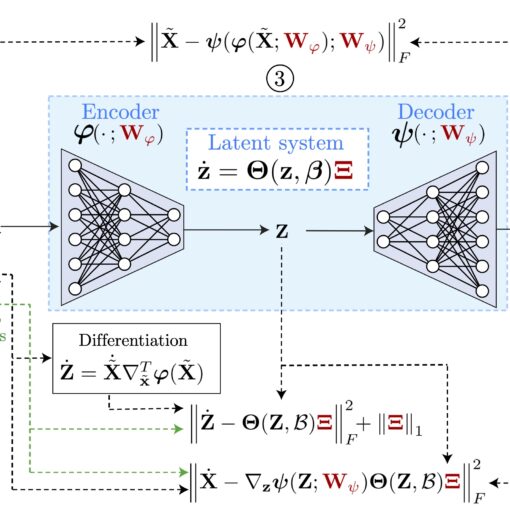
A new MOX Report entitled “Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions” by Conti, […]
A new MOX Report entitled “Stratified Multilevel Graphical Models: Examining Gender Dynamics in Education” by Nicolussi, F.; Masci, C. has appeared in […]