A new MOX Report entitled “Sobolev–Poincaré inequalities for piecewise $W^{1,p}$ functions over general polytopic meshes” by Botti, M.; Mascotto, L. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/17-2025.pdf
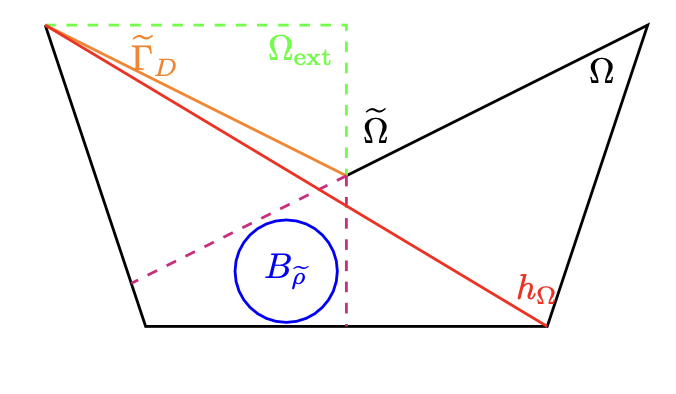
Abstract: We establish Sobolev-Poincaré inequalities for piecewise $W^{1,p}$ functions over sequences of fairly general polytopic (thence also shape-regular simplicial and Cartesian) meshes in any dimension; amongst others, they cover the case of standard Poincaré inequalities for piecewise $W^{1,p}$ functions and can be useful in the analysis of nonconforming finite element discretizations of nonlinear problems. Crucial tools in their derivation are novel Sobolev-trace inequalities and Babuska-Aziz inequalities with mixed boundary conditions. We provide estimates that are constant free, i.e., that are fully explicit with respect to the geometric properties of the domain and the underlying sequence of polytopic meshes.