A new MOX Report entitled “A structure-preserving LDG discretization of the Fisher-Kolmogorov equation for modeling neurodegenerative diseases” by Antonietti, P.F.; Corti, M.; Gómez, S.; Perugia, I. has appeared in the MOX Report Collection.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/18-2025.pdf
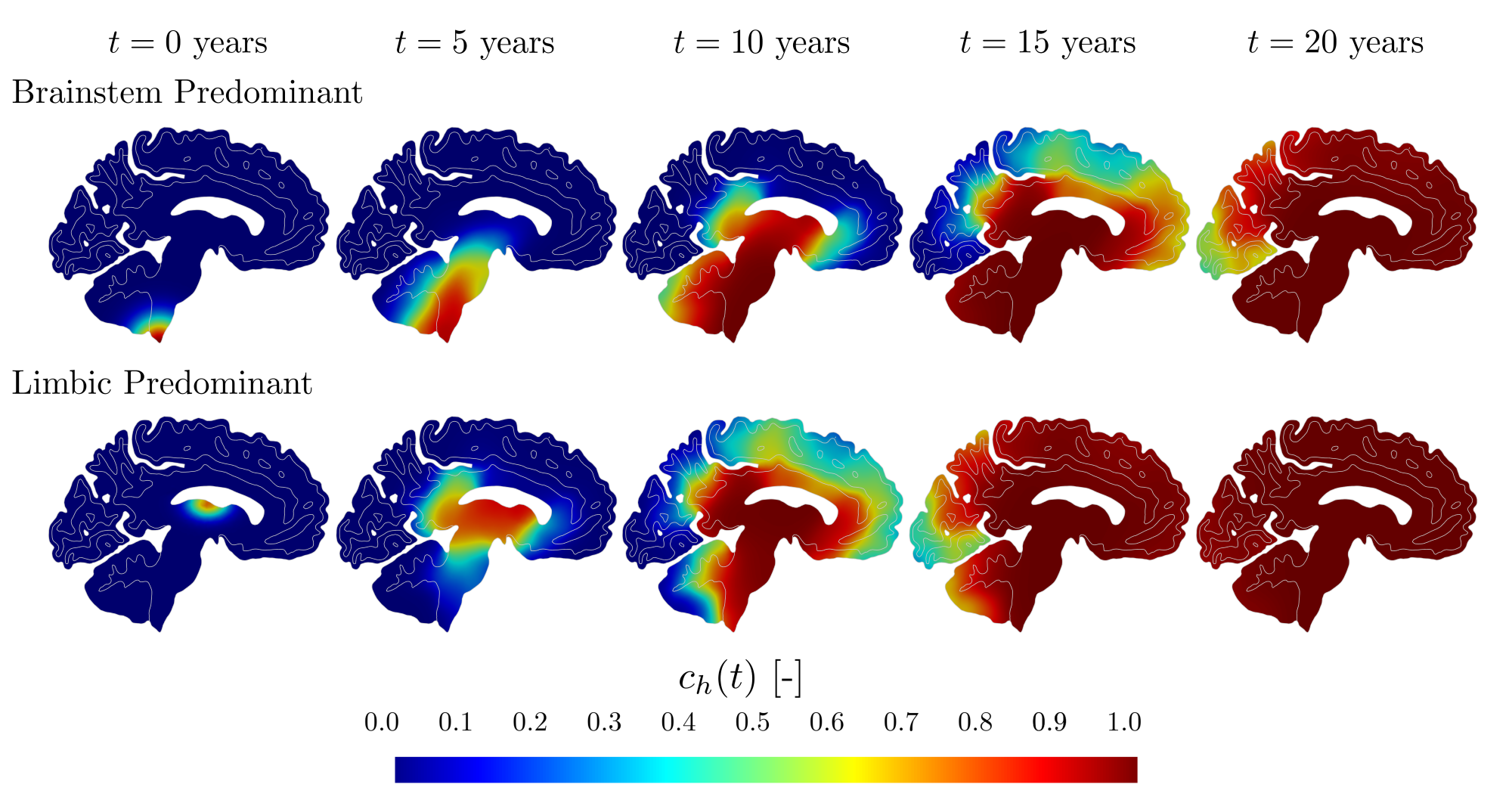
Abstract: This work presents a structure-preserving, high-order, unconditionally stable numerical method for approximating the solution to the Fisher-Kolmogorov equation on polytopic meshes, with a particular focus on its application in simulating misfolded protein spreading in neurodegenerative diseases. The model problem is reformulated using an entropy variable to guarantee solution positivity, boundedness, and satisfaction of a discrete entropy-stability inequality at the numerical level. The scheme combines a local discontinuous Galerkin method on polytopal meshes for the space discretization with a v-step backward differentiation formula for the time integration. Implementation details are discussed, including a detailed derivation of the linear systems arising from Newton’s iteration. The accuracy and robustness of the proposed method are demonstrated through extensive numerical tests. Finally, the method’s practical performance is demonstr! ated thro ugh simulations of alpha-synuclein propagation in a two-dimensional brain geometry segmented from MRI data, providing a relevant computational framework for modeling synucleopathies (such as Parkinson’s disease) and, more generally, neurodegenerative diseases.