A new MOX Report entitled “Polytopal discontinuous Galerkin methods for low-frequency poroelasticity coupled to unsteady Stokes flow” by Botti, M.; Fumagalli, I.; Mazzieri, I. has appeared in the MOX Report Collection of the @mox_lab –@dipartimento di matematica, @polimi.
Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/08-2025.pdf
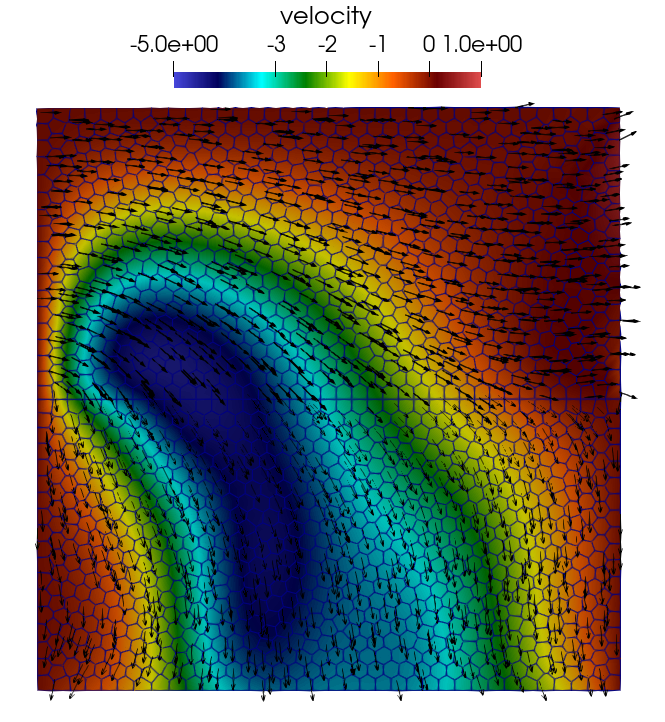
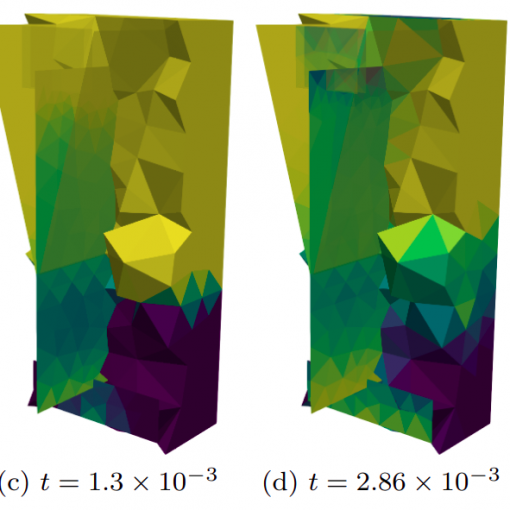
Abstract: We focus on the numerical analysis of a polygonal discontinuous Galerkin scheme for the simulation of the exchange of fluid between a deformable saturated poroelastic structure and an adjacent free-flow channel. We specifically address wave phenomena described by the low-frequency Biot model in the poroelastic region and unsteady Stokes flow in the open channel, possibly an isolated cavity or a connected fracture system. The coupling at the interface between the two regions is realized by means of transmission conditions expressing conservation laws. The spatial discretization hinges on the weak form of the two-displacement poroelasticity system and a stress formulation of the Stokes equation with weakly imposed symmetry. We present a complete stability analysis for the proposed semi-discrete formulation and derive a-priori hp-error estimates.