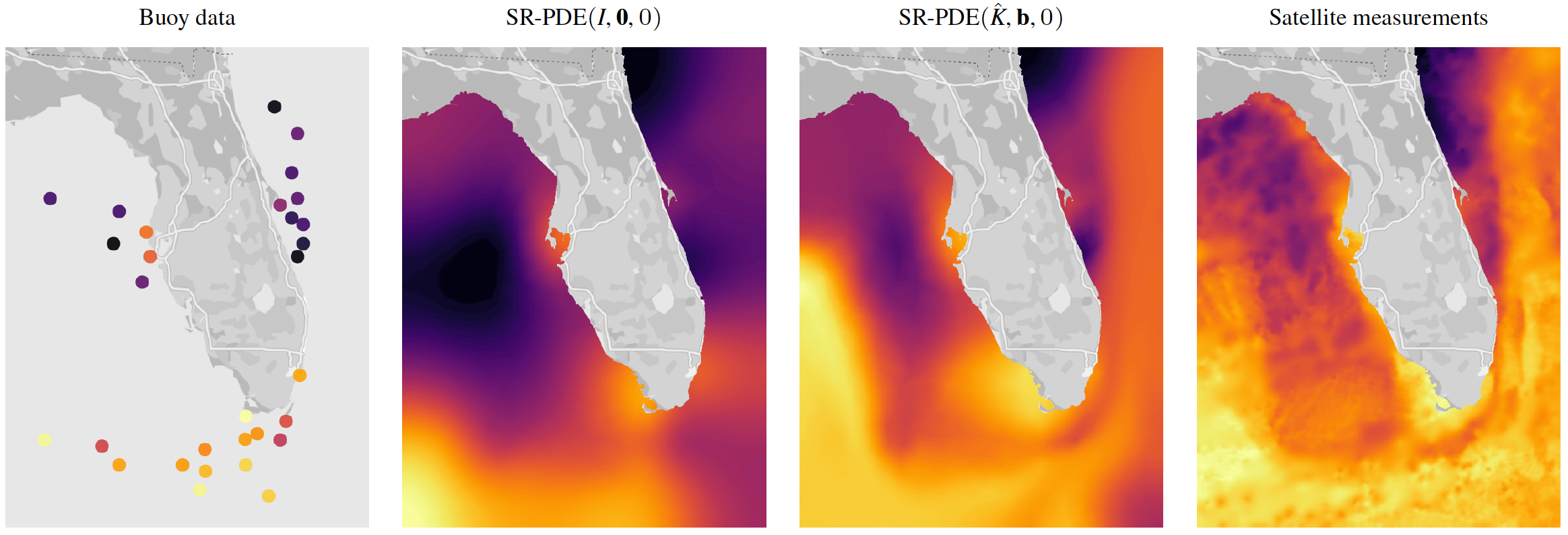
A new MOX Report entitled “Modeling anisotropy and non-stationarity through physics-informed spatial regression” by Tomasetto, M.; Arnone, E.; Sangalli, L.M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/90-2024.pdf Abstract: Many spatially dependent phenomena, that are of interest in environmental problems, are characterized by strong anisotropy and non-stationarity. Moreover, the data are often observed over regions with complex conformations, such as water bodies with complicated shorelines, or regions with complex orography. Furthermore, the distribution of the data locations may be strongly inhomogeneous over space. These issues may challenge popular approaches to spatial data analysis. In this work, we show how we can accurately address these issues by spatial regression with differential regularization. We model the spatial variation by a Partial Differential Equation (PDE), defined upon the considered spatial domain. This PDE may depend upon some unknown parameters, that we estimate from the data, through an appropriate profiling estimation approach. The PDE may encode some available problem-specific information on the considered phenomenon, and permits a rich! modeling of anisotropy and non-stationarity. The performances of the proposed approach are compared to competing methods, through simulation studies and real data applications. In particular, we analyse rainfall data over Switzerland, characterized by strong anisotropy, and oceanographic data in the Gulf of Mexico, characterized by non-stationarity due to the Gulf Stream.
You may also like
A new MOX Report entitled “Two new calibration techniques of lumped-parameter mathematical models for the cardiovascular system” by Tonini, A., Regazzoni, F., […]
A new MOX Report entitled “Deep learning-based reduced order models for the real-time simulation of the nonlinear dynamics of microstructures” by Fresca, […]
A new MOX Report entitled “Reduced order modeling of parametrized systems through autoencoders and SINDy approach: continuation of periodic solutions” by Conti, […]
A new MOX Report entitled “Application of Deep Learning Reduced-Order Modeling for Single-Phase Flow in Faulted Porous Media” by Enrico Ballini e […]