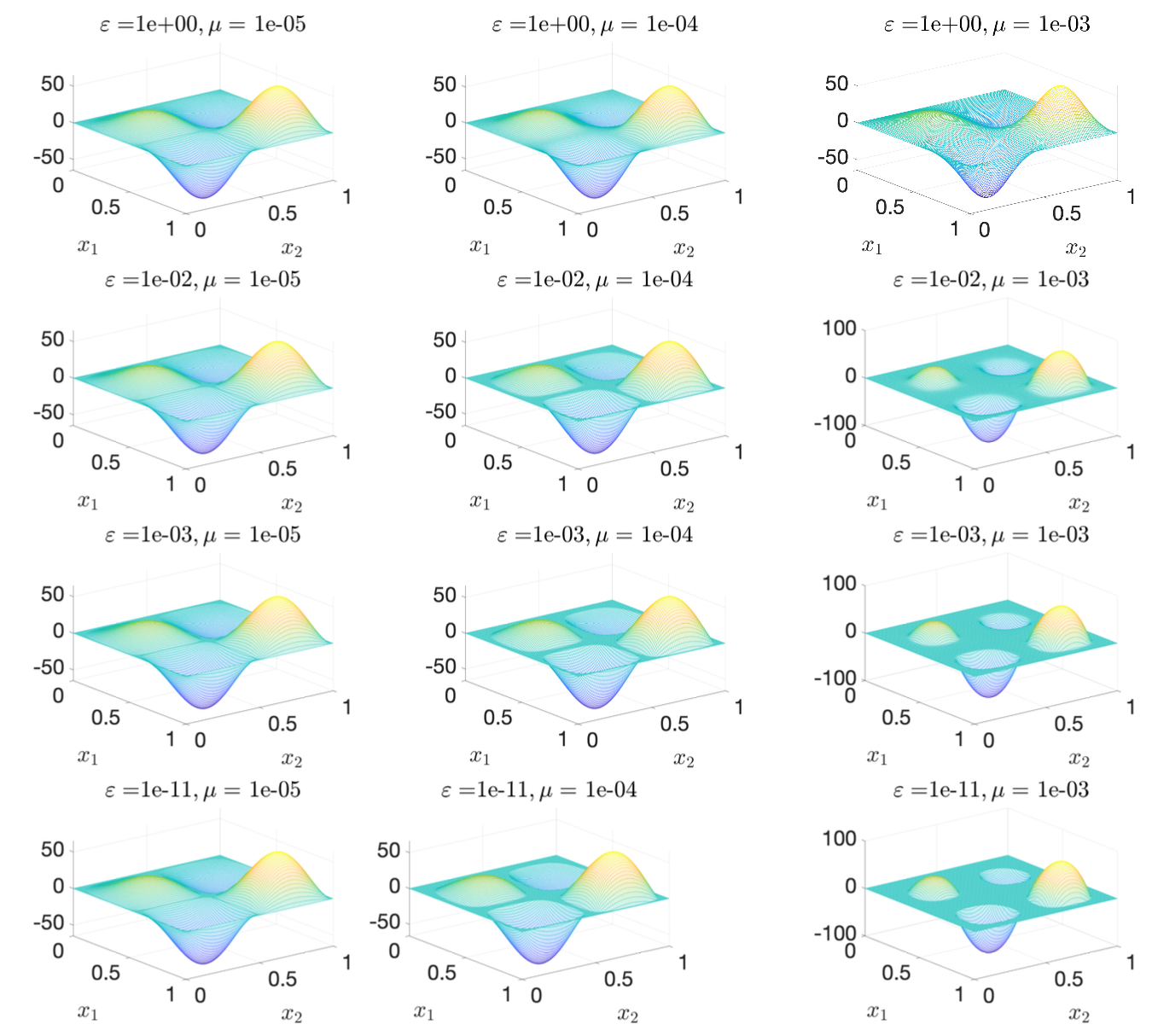
A new MOX Report entitled “Solving Semi-Linear Elliptic Optimal Control Problems with L1-Cost via Regularization and RAS-Preconditioned Newton Methods” by Ciaramella, G.; Kartmann, M.; Mueller, G. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/91-2024.pdf Abstract: We present a new parallel computational framework for the efficient solution of a class of L2/L1-regularized optimal control problems governed by semi-linear elliptic partial differential equations (PDEs). The main difficulty in solving this type of problem is the nonlinearity and non-smoothness of the L1-term in the cost functional, which we address by employing a combination of several tools. First, we approximate the non-differentiable projection operator appearing in the optimality system by an appropriately chosen regularized operator and establish convergence of the resulting system solutions. Second, we apply a continuation strategy to control the regularization parameter to improve the behavior of (damped) Newton methods. Third, we combine Newton’s method with a domain-decomposition-based nonlinear preconditioning, which improves its robustness properties and allows for parallelization. The efficiency of the proposed numerical framework! is demon strated by extensive numerical experiments.
You may also like
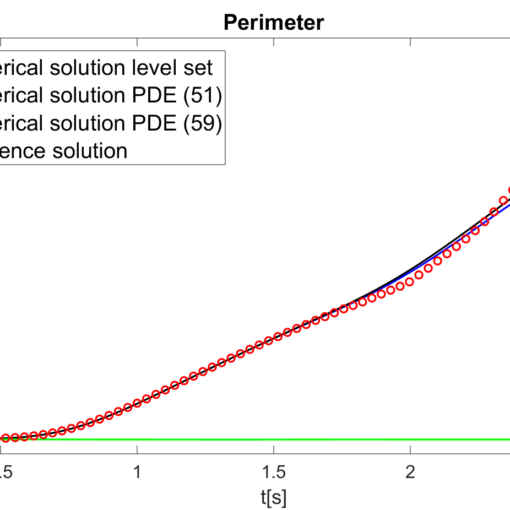
A new MOX report entitled “On the evolution equations of interfacial variables in two-phase flows” by Orlando, G; Barbante, P.F.; Bonaventura, L. […]
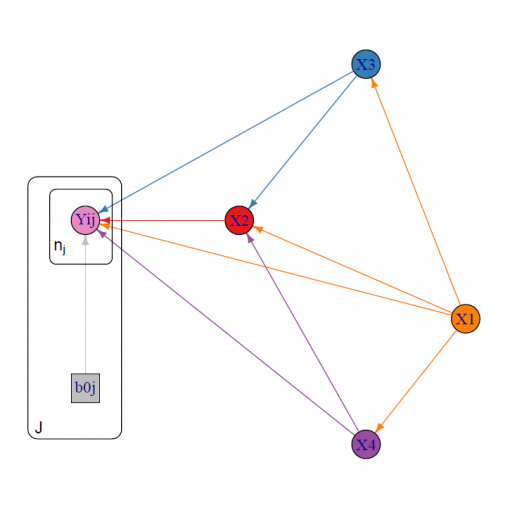
A new MOX Report entitled “Stratified Multilevel Graphical Models: Examining Gender Dynamics in Education” by Nicolussi, F.; Masci, C. has appeared in […]
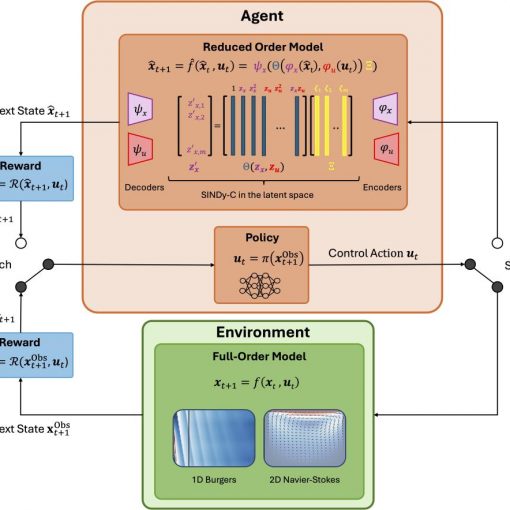
A new MOX Report entitled “Interpretable and efficient data-driven discovery and control of distributed systems” by Wolf, F.; Botteghi, N.; Fasel, U.; […]
A new MOX Report entitled “Anatomically compliant modes of variations: new tools for brain connectivity” by Clementi, L.; Arnone, E.; Santambrogio, M.D.; […]