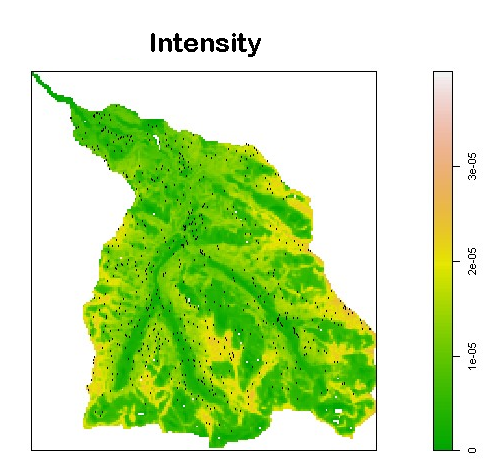
A new MOX Report entitled “An interpretable and transferable model for shallow landslides detachment combining spatial Poisson point processes and generalized additive models” by Patanè, G.; Bortolotti, T.; Yordanov, V.; Biagi, L. G. A.; Brovelli, M. A.; Truong, A. Q; Vantini, S. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/72-2024.pdf Abstract: Less than 10 meters deep, shallow landslides are rapidly moving and strongly dangerous slides. In the present work, the probabilistic distribution of the landslide detachment points within a valley is modelled as a spatial Poisson point process, whose intensity depends on geophysical predictors according to a generalized additive model. Modelling the intensity with a generalized additive model jointly allows to obtain good predictive performance and to preserve the interpretability of the effects of the geophysical predictors on the intensity of the process. We propose a novel workflow, based on Random Forests, to select the geophysical predictors entering the model for the intensity. In this context, the statistically significant effects are interpreted as activating or stabilizing factors for landslide detachment. In order to guarantee the transferability of the resulting model, training, validation, and test of the algorithm are performed on m! utually d isjoint valleys in the Alps of Lombardy (Italy). Finally, the uncertainty around the estimated intensity of the process is quantified via semiparametric bootstrap.
You may also like
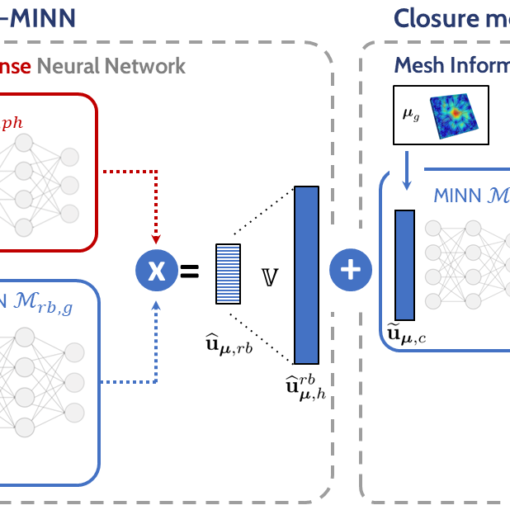
A new MOX Report entitled “Nonlinear model order reduction for problems with microstructure using mesh informed neural networks” by Vitullo, P.; Colombo, […]
A new MOX Report entitled “Ask Your Data—Supporting Data Science Processes by Combining AutoML and Conversational Interfaces” by Pidò, S.; Pinoli, P.; […]
A new MOX Report entitled “A Virtual Element method for non-Newtonian fluid flows” by Antonietti, P.F.; Beirao da Veiga, L.; Botti, M.; […]
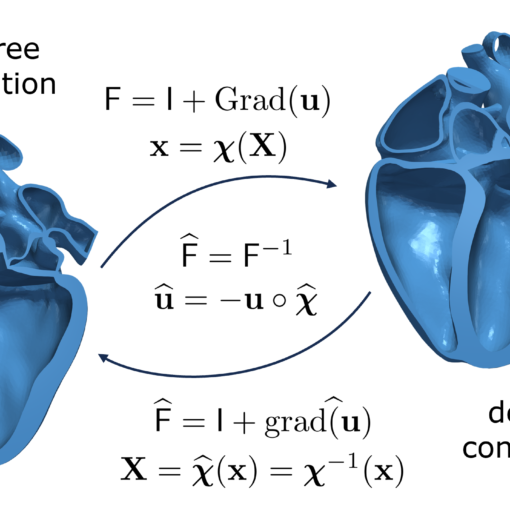
A new MOX Report entitled “Reconstructing relaxed configurations in elastic bodies: mathematical formulation and numerical methods for cardiac modeling” by Barnafi, N. […]