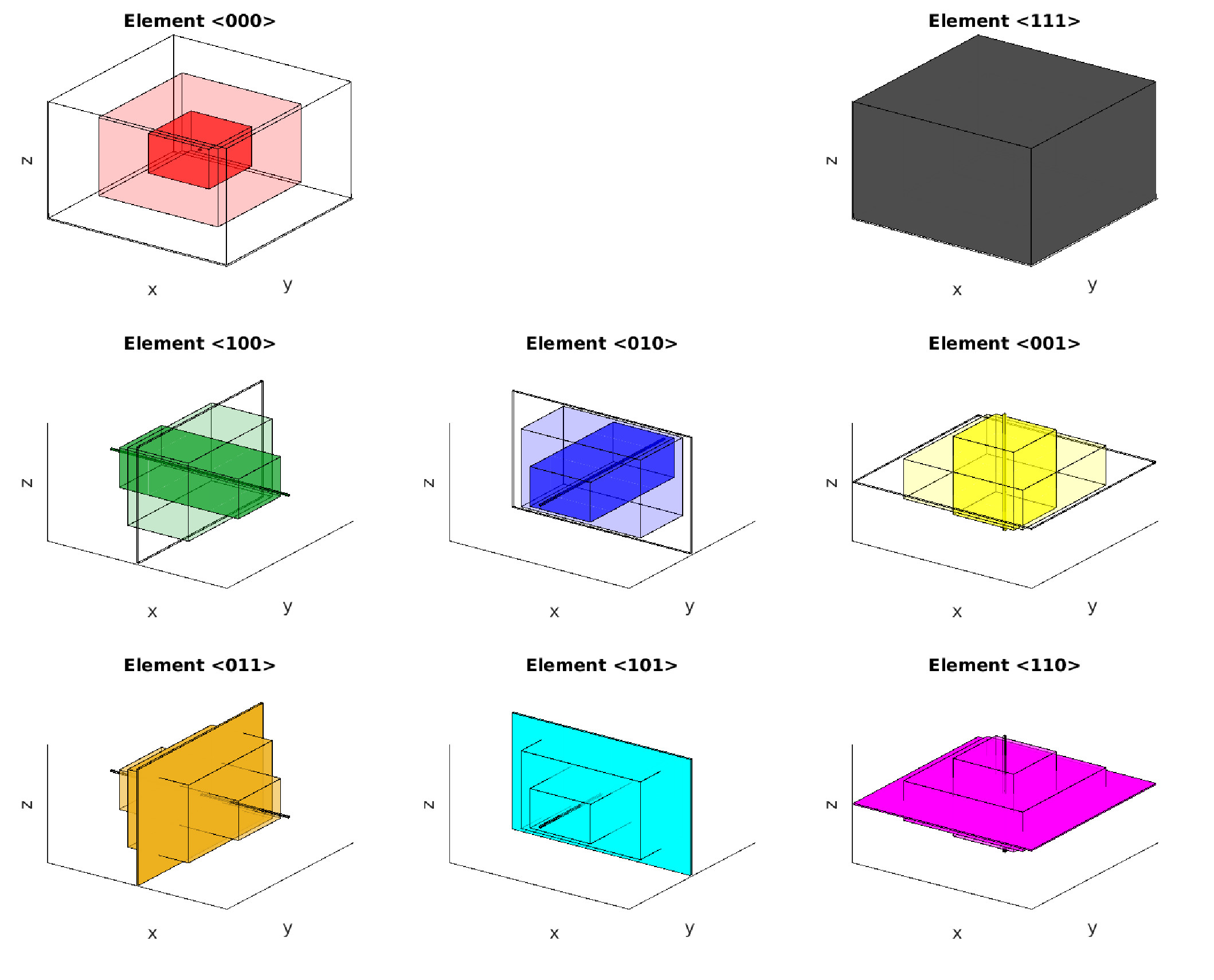
A new MOX Report entitled “Schwarz Waveform Relaxation and the Unmapped Tent-Pitching Method in 3D” by Artoni, A.; Ciaramella, G.; Gander, M.J.; Mazzieri, I. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/55-2024.pdf Abstract: Several Parallel-in-Time (PinT) algorithms, especially multilevel methods like Parareal and MGRIT, struggle when applied to hyperbolic partial differential equations. There are however also very effective PinT methods for hyperbolic problems which use the hyperbolic nature of the problem to their advantage. Typical examples are Schwarz Waveform Relaxation methods, and the Mapped and Unmapped Tent Pitching methods. We present and study here for the first time the Unmapped Tent Pitching method in three spatial dimensions, applied to a second order wave equation. We give a general equivalence result with the Mapped Tent Pitching algorithm using Schwarz Waveform Relaxation to build the link, and also characterize in detail the resulting 4D space-time tents generated implicitly by the Unmapped Tent Pitching method. This leads to a complete convergence analysis of the method in 3D.
You may also like
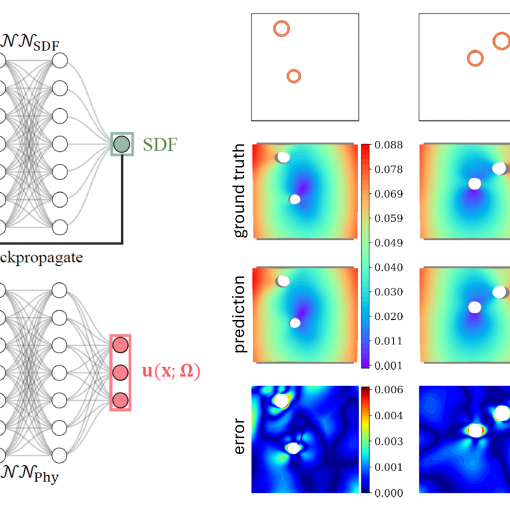
A new MOX Report entitled “Shape-informed surrogate models based on signed distance function domain encoding” by Zhang, L.; Pagani, S.; Zhang, J.; […]
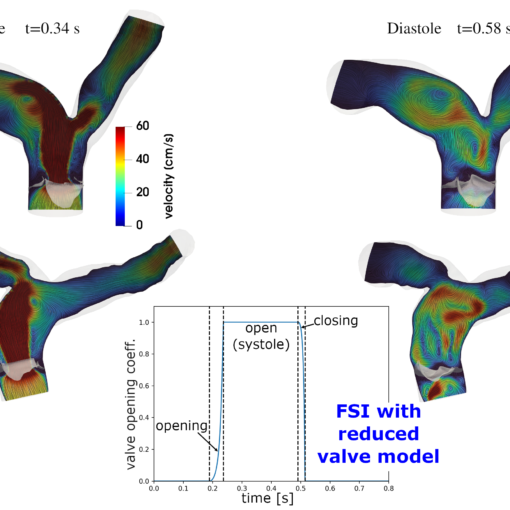
A new MOX Report entitled “Computational haemodynamics for pulmonary valve replacement by means of a reduced Fluid-Structure Interaction model” by Criseo, M.; […]
A new MOX Report entitled “Trace inequalities for piecewise W^1,p functions over general polytopic meshes ” by Botti, M.; Mascotto, L. has […]
A new MOX Report entitled “Patient-specific prediction of glioblastoma growth via reduced order modeling and neural networks” by Cerrone, D.; Riccobelli, D.; […]