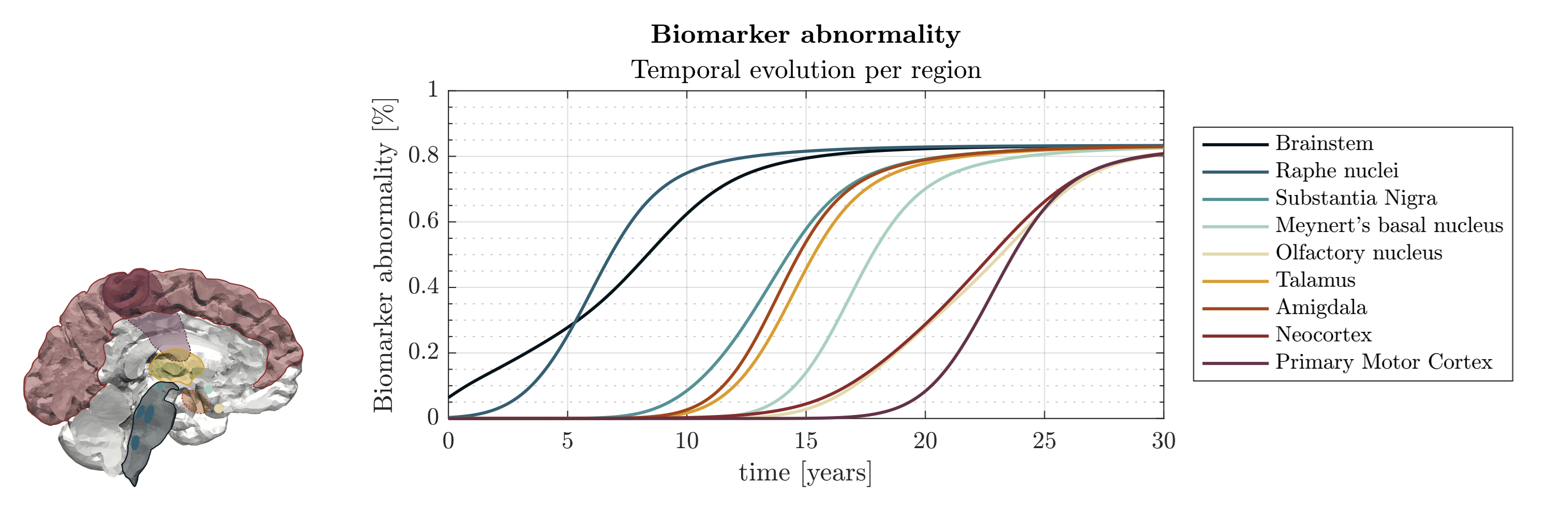
A new MOX Report entitled “A discontinuous Galerkin method for the three-dimensional heterodimer model with application to prion-like proteins’ dynamics” by Antonietti, P.F.; Corti, M.; Lorenzon, G. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/51-2024.pdf Abstract: Neurocognitive disorders, such as Alzheimer’s and Parkinson’s, have a wide social impact. These proteinopathies involve misfolded proteins accumulating into neurotoxic aggregates. Mathematical and computational models describing the prion-like dynamics offer an analytical basis to study the diseases’ evolution and a computational framework for exploring potential therapies. This work focuses on the heterodimer model in a three-dimensional setting, a reactive-diffusive system of nonlinear partial differential equations describing the evolution of both healthy and misfolded proteins. We investigate traveling wave solutions and diffusion-driven instabilities as a mechanism of neurotoxic pattern formation. For the considered mathematical model, we propose a space discretization, relying on the Discontinuous Galerkin method on polytopal/polyhedral grids, allowing high-order accuracy and flexible handling of the complicated brain’s geometry. Furthe! r, we pre sent a-priori error estimates for the semi-discrete formulation and we perform convergence tests to verify the theoretical results. Finally, we conduct simulations using realistic data on a three-dimensional brain mesh reconstructed from medical images.
You may also like
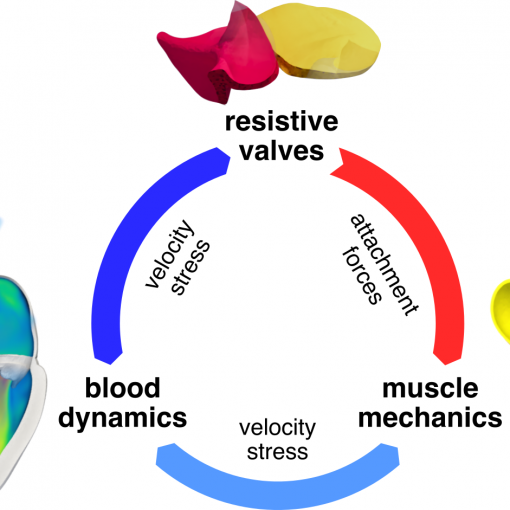
A new MOX Report entitled “Coupling models of resistive valves to muscle mechanics in cardiac fluid-structure interaction simulations” by Bucelli, M.; Dede’, […]
A new MOX Report entitled “A comprehensive stroke risk assessment by combining atrial computational fluid dynamics simulations and functional patient data” by […]
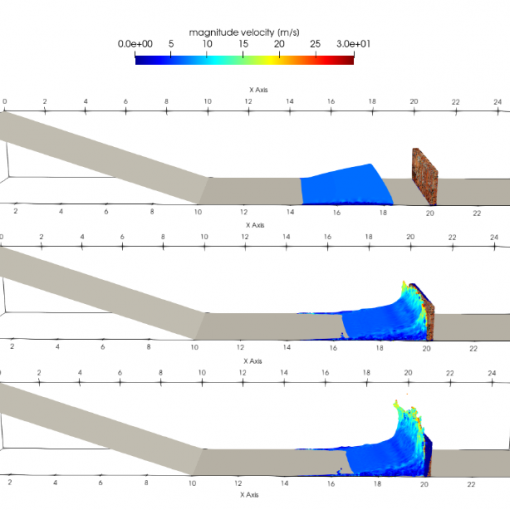
A new MOX Report entitled “Landslide run-out simulations with depth-averaged models and integration with 3D impact analysis using the Material Point Method” […]
A new MOX Report entitled “Unified discontinuous Galerkin analysis of a thermo/poro-viscoelasticity model” by Bonetti, S.; Corti, M. has appeared in the […]