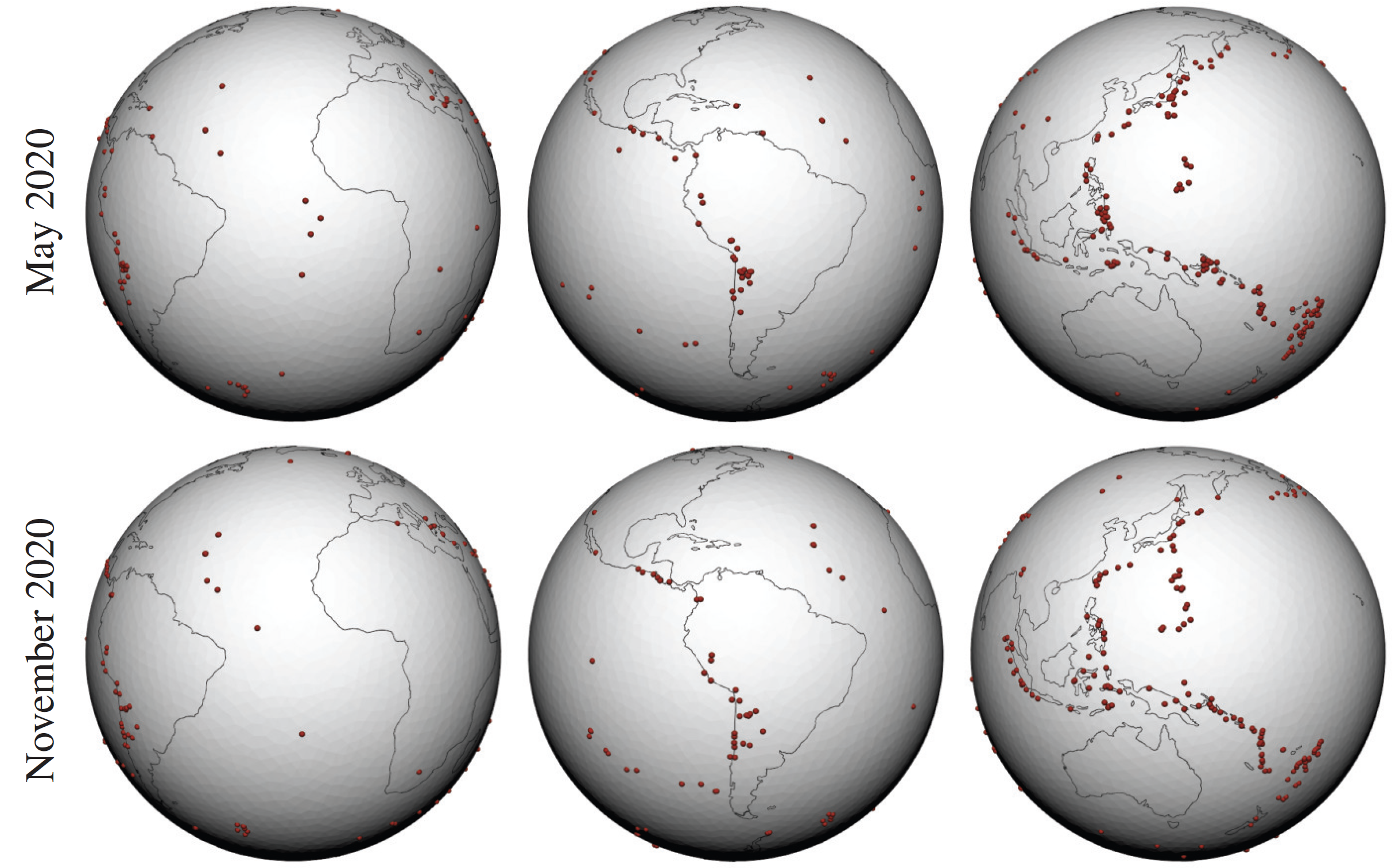
A new MOX Report entitled “A nonparametric penalized likelihood approach to density estimation of space-time point patterns” by Begu, B.; Panzeri, S.; Arnone, E.; Carey, M.; Sangalli, L.M. has appeared in the MOX Report Collection. Check it out here: https://www.mate.polimi.it/biblioteca/add/qmox/37-2024.pdf Abstract: In this work, we consider space-time point processes and study their continuous space-time evolution. We propose an innovative nonparametric methodology to estimate the unknown space-time density of the point pattern, or, equivalently, to estimate the intensity of an inhomogeneous space-time Poisson point process. The presented approach combines maximum likelihood estimation with roughness penalties, based on differential operators, defined over the spatial and temporal domains of interest. We first establish some important theoretical properties of the considered estimator, including its consistency. We then develop an efficient and flexible estimation procedure that leverages advanced numerical and computation techniques. Thanks to a discretization based on finite elements in space and B–splines in time, the proposed method can effectively capture complex multi-modal and strongly anisotropic spatio-temporal point patterns; moreover, these point patterns may be observed o! ver plana r or curved domains with non-trivial geometries, due to geographic constraints, such as coastal regions with complicated shorelines, or curved regions with complex orography. In addition to providing estimates, the method’s functionalities also include the introduction of appropriate uncertainty quantification tools. We thoroughly validate the proposed method, by means of simulation studies and applications to real-world data. The obtained results highlight significant advantages over state-of-the-art competing approaches.
You may also like
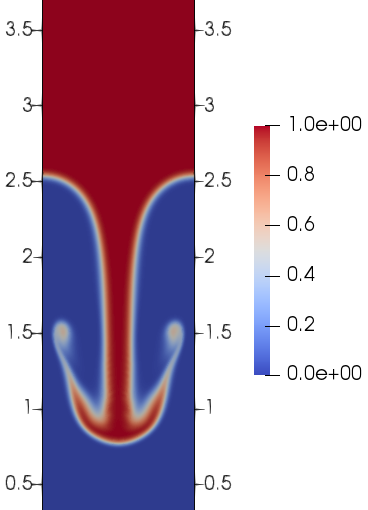
A new MOX report entitled “An implicit DG solver for incompressible two-phase flows with an artificial compressibility formulation” by Orlando, G. has […]
A new MOX Report entitled “Enhanched uncertainty quantification variational autoencoders for the solution of Bayesian inverse problems” by Tonini, A.; Dede’, L. […]
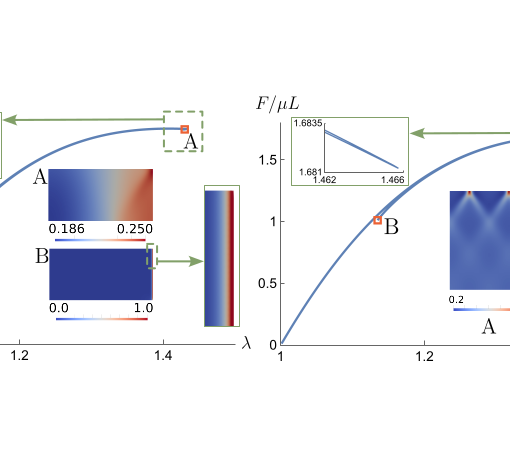
A new MOX Report entitled “Elastic Instability behind Brittle Fracture” by Riccobelli, D.; Ciarletta, P.; Vitale, G.; Maurini, C.; Truskinovsky, L. has […]
A new MOX Report entitled “Polytopal discontinuous Galerkin methods for low-frequency poroelasticity coupled to unsteady Stokes flow” by Botti, M.; Fumagalli, I.; […]